DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Euler's Equations for Rotations in the Body-Fixed Frame

Suppose now that the body-fixed frame is rotating in the space-fixed frame with angular velocity $ \underline{\omega}$. Then the total torque on the rigid body becomes [270]

$\displaystyle \underline{\tau}\eqsp \dot{\underline{L}} + \underline{\omega}\times \underline{L}. \protect$ (B.30)

Similarly, the total external forces on the center of mass become

$\displaystyle \underline{f}\eqsp \dot{\underline{p}} + \underline{\omega}\times\underline{p}. $

If the body-fixed frame is aligned with the principal axes of rotation (§B.4.16), then the mass moment of inertia tensor is diagonal, say $ \mathbf{I}=$diag$ (I_1,I_2,I_3)$. In this frame, the angular momentum is simply

$\displaystyle \underline{L}\eqsp \left[\begin{array}{c} I_1\omega_1 \\ [2pt] I_2\omega_2 \\ [2pt] I_3\omega_3\end{array}\right] $

so that the term $ \underline{\omega}\times\underline{L}$ becomes (cf. Eq.$ \,$(B.15))

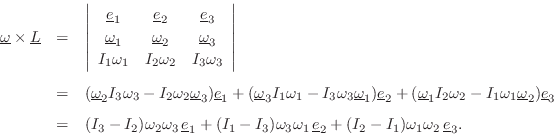
\begin{eqnarray*} \underline{\omega}\times\underline{L}&=& \left\vert \begin{arr... ...1\,\underline{e}_2 + (I_2-I_1)\omega_1\omega_2\,\underline{e}_3. \end{eqnarray*}

Substituting this result into Eq.$ \,$(B.30), we obtain the following equations of angular motion for an object rotating in the body-fixed frame defined by its three principal axes of rotation:

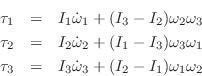
\begin{eqnarray*} \tau_1 &=& I_1 \dot{\omega}_1 + (I_3-I_2)\omega_2\omega_3\\ \... ...a_1\\ \tau_3 &=& I_3 \dot{\omega}_3 + (I_2-I_1)\omega_1\omega_2 \end{eqnarray*}

These are call Euler's equations:B.29Since these equations are in the body-fixed frame, $ I_i$ is the mass moment of inertia about principal axis $ i$, and $ \omega_i$ is the angular velocity about principal axis $ i$.

Next Section:
Examples
Previous Section:
Angular Motion in the Space-Fixed Frame