The Bow-String Scattering Junction
The theory of bow-string interaction is described in
[95,151,244,307,308]. The basic
operation of the bow is to reconcile the nonlinear bow-string friction
curve ![]() with the string wave impedance
with the string wave impedance ![]() :
:

or, equating these equal and opposite forces, we obtain
![\includegraphics[width=4in]{eps/fBowFrictionCurve}](http://www.dsprelated.com/josimages_new/pasp/img2570.png) |
In a bowed string simulation as in Fig.9.51, a velocity input (which is injected equally in the left- and right-going directions) must be found such that the transverse force of the bow against the string is balanced by the reaction force of the moving string. If bow-hair dynamics are neglected [176], the bow-string interaction can be simulated using a memoryless table lookup or segmented polynomial in a manner similar to single-reed woodwinds [431].
A derivation analogous to that for the single reed is possible for the
simulation of the bow-string interaction. The final result is as follows.
where
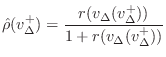
Nominally,
![]() is constant (the so-called static coefficient
of friction) for
is constant (the so-called static coefficient
of friction) for
![]() , where
, where
![]() is both the
capture and break-away differential velocity. For
is both the
capture and break-away differential velocity. For
![]() ,
,
![]() falls quickly to a low dynamic coefficient of friction. It
is customary in the bowed-string physics literature to assume that the
dynamic coefficient of friction continues to approach zero with increasing
falls quickly to a low dynamic coefficient of friction. It
is customary in the bowed-string physics literature to assume that the
dynamic coefficient of friction continues to approach zero with increasing
![]() [308,95].
[308,95].
Figure 9.54 illustrates a simplified, piecewise linear
bow table
![]() . The flat center portion corresponds to a
fixed reflection coefficient ``seen'' by a traveling wave encountering
the bow stuck against the string, and the outer sections of the curve
give a smaller reflection coefficient corresponding to the reduced
bow-string interaction force while the string is slipping under the
bow. The notation
. The flat center portion corresponds to a
fixed reflection coefficient ``seen'' by a traveling wave encountering
the bow stuck against the string, and the outer sections of the curve
give a smaller reflection coefficient corresponding to the reduced
bow-string interaction force while the string is slipping under the
bow. The notation
![]() at the corner point denotes the capture or
break-away differential velocity. Note that hysteresis is neglected.
at the corner point denotes the capture or
break-away differential velocity. Note that hysteresis is neglected.
Next Section:
Bowed String Synthesis Extensions
Previous Section:
Digital Waveguide Bowed-String








![\includegraphics[width=4in]{eps/fBowTable}](http://www.dsprelated.com/josimages_new/pasp/img2581.png)











