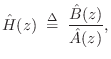Digital Filter Design Overview
This section (adapted from [428]), summarizes some of the more commonly used methods for digital filter design aimed at matching a nonparametric frequency response, such as typically obtained from input/output measurements. This problem should be distinguished from more classical problems with their own specialized methods, such as designing lowpass, highpass, and bandpass filters [343,362], or peak/shelf equalizers [559,449], and other utility filters designed from a priori mathematical specifications.
The problem of fitting a digital filter to a prescribed frequency
response may be formulated as follows. To simplify, we set ![]() .
.
Given a continuous complex function
![]() ,
corresponding to a causal desired frequency response,9.8 find a stable digital filter of the form
,
corresponding to a causal desired frequency response,9.8 find a stable digital filter of the form
| (9.15) | |||
| (9.16) |
with
![]() given, such that some norm of the error
given, such that some norm of the error
is minimum with respect to the filter coefficients
The approximate filter ![]() is typically constrained to be
stable, and since
is typically constrained to be
stable, and since
![]() is causal (no positive powers of
is causal (no positive powers of ![]() ),
stability implies causality. Consequently, the impulse response of the
model
),
stability implies causality. Consequently, the impulse response of the
model
![]() is zero for
is zero for ![]() .
.
The filter-design problem is then to find a (strictly) stable
![]() -pole,
-pole,
![]() -zero digital filter which minimizes some norm of
the error in the frequency-response. This is fundamentally
rational approximation of a complex function of a real
(frequency) variable, with constraints on the poles.
-zero digital filter which minimizes some norm of
the error in the frequency-response. This is fundamentally
rational approximation of a complex function of a real
(frequency) variable, with constraints on the poles.
While the filter-design problem has been formulated quite naturally,
it is difficult to solve in practice. The strict stability assumption
yields a compact space of filter coefficients
![]() , leading to the
conclusion that a best approximation
, leading to the
conclusion that a best approximation
![]() exists over this
domain.9.9Unfortunately, the norm of the error
exists over this
domain.9.9Unfortunately, the norm of the error
![]() typically is
not a convex9.10function of the filter coefficients on
typically is
not a convex9.10function of the filter coefficients on
![]() . This
means that algorithms based on gradient descent may fail to find an
optimum filter due to their premature termination at a suboptimal
local minimum of
. This
means that algorithms based on gradient descent may fail to find an
optimum filter due to their premature termination at a suboptimal
local minimum of
![]() .
.
Fortunately, there is at least one norm whose global minimization may be accomplished in a straightforward fashion without need for initial guesses or ad hoc modifications of the complex (phase-sensitive) IIR filter-design problem--the Hankel norm [155,428,177,36]. Hankel norm methods for digital filter design deliver a spontaneously stable filter of any desired order without imposing coefficient constraints in the algorithm.
An alternative to Hankel-norm approximation is to reformulate the
problem, replacing Eq.![]() (8.17) with a modified error criterion so that
the resulting problem can be solved by linear least-squares or
convex optimization techniques. Examples include
(8.17) with a modified error criterion so that
the resulting problem can be solved by linear least-squares or
convex optimization techniques. Examples include
- Pseudo-norm minimization:
(Pseudo-norms can be zero for nonzero functions.)
For example, Padé approximation falls in this category.
In Padé approximation, the first
 samples
of the impulse-response
samples
of the impulse-response 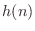 of
of 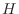 are matched exactly,
and the error in the remaining impulse-response samples is ignored.
are matched exactly,
and the error in the remaining impulse-response samples is ignored.
- Ratio Error: Minimize
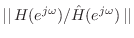 subject to
subject to
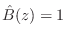 . Minimizing the
. Minimizing the  norm of the ratio error
yields the class of methods known as linear prediction
techniques [20,296,297]. Since,
by the definition of a norm, we have
norm of the ratio error
yields the class of methods known as linear prediction
techniques [20,296,297]. Since,
by the definition of a norm, we have
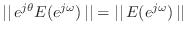 ,
it follows that
,
it follows that
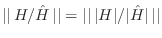 ; therefore,
ratio error methods ignore the phase of the
approximation. It is also evident that ratio error is
minimized by making
; therefore,
ratio error methods ignore the phase of the
approximation. It is also evident that ratio error is
minimized by making
 larger than
larger than
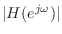 .9.11 For this reason, ratio-error
methods are considered most appropriate for modeling the
spectral envelope of
.9.11 For this reason, ratio-error
methods are considered most appropriate for modeling the
spectral envelope of
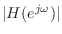 . It is well known
that these methods are fast and exceedingly robust in
practice, and this explains in part why they are used almost
exclusively in some data-intensive applications such as speech
modeling and other spectral-envelope applications. In some
applications, such as adaptive control or forecasting, the
fact that linear prediction error is minimized can justify
their choice.
. It is well known
that these methods are fast and exceedingly robust in
practice, and this explains in part why they are used almost
exclusively in some data-intensive applications such as speech
modeling and other spectral-envelope applications. In some
applications, such as adaptive control or forecasting, the
fact that linear prediction error is minimized can justify
their choice.
- Equation error: Minimize
When the
![$\displaystyle \left\Vert\,{\hat A}(e^{j\omega})H(e^{j\omega})-{\hat B}(e^{j\ome...
...}(e^{j\omega})\left[ H(e^{j\omega})-{\hat H}(e^{j\omega})\right]\,\right\Vert.
$](http://www.dsprelated.com/josimages_new/pasp/img1848.png)
 norm of equation-error is minimized, the
problem becomes solving a set of
norm of equation-error is minimized, the
problem becomes solving a set of
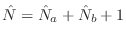 linear
equations.
linear
equations.
The above expression makes it clear that equation-error can be seen as a frequency-response error weighted by
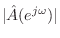 . Thus, relatively large errors can be
expected where the poles of the optimum approximation (roots
of
. Thus, relatively large errors can be
expected where the poles of the optimum approximation (roots
of
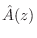 ) approach the unit circle
) approach the unit circle 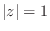 . While this may
make the frequency-domain formulation seem ill-posed, in the
time-domain, linear prediction error is minimized in
the
. While this may
make the frequency-domain formulation seem ill-posed, in the
time-domain, linear prediction error is minimized in
the  sense, and in certain applications this is ideal.
(Equation-error methods thus provide a natural extension of
ratio-error methods to include zeros.) Using so-called
Steiglitz-McBride iterations
[287,449,288], the
equation-error solution iteratively approaches the
norm-minimizing solution of Eq.
sense, and in certain applications this is ideal.
(Equation-error methods thus provide a natural extension of
ratio-error methods to include zeros.) Using so-called
Steiglitz-McBride iterations
[287,449,288], the
equation-error solution iteratively approaches the
norm-minimizing solution of Eq. (8.17) for the L2
norm.
(8.17) for the L2
norm.
Examples of minimizing equation error using the matlab function invfreqz are given in §8.6.3 and §8.6.4 below. See [449, Appendix I] (based on [428, pp. 48-50]) for a discussion of equation-error IIR filter design and a derivation of a fast equation-error method based on the Fast Fourier Transform (FFT) (used in invfreqz).
- Conversion to real-valued approximation: For
example, power spectrum matching, i.e., minimization of
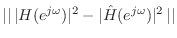 , is possible
using the Chebyshev or
, is possible
using the Chebyshev or
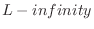 norm [428]. Similarly,
linear-phase filter design can be carried out with some
guarantees, since again the problem reduces to real-valued
approximation on the unit circle. The essence of these
methods is that the phase-response is eliminated from
the error measure, as in the norm of the ratio error, in order
to convert a complex approximation problem into a real one.
Real rational approximation of a continuous curve appears to
be solved in principle only under the
norm [428]. Similarly,
linear-phase filter design can be carried out with some
guarantees, since again the problem reduces to real-valued
approximation on the unit circle. The essence of these
methods is that the phase-response is eliminated from
the error measure, as in the norm of the ratio error, in order
to convert a complex approximation problem into a real one.
Real rational approximation of a continuous curve appears to
be solved in principle only under the
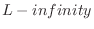 norm
[373,374].
norm
[373,374].
- Decoupling poles and zeros: An effective example of
this approach is Kopec's method [428] which consists of
using ratio error to find the poles, computing the error
spectrum
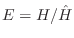 , inverting it, and fitting poles again (to
, inverting it, and fitting poles again (to
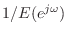 ). There is a wide variety of methods which first
fit poles and then zeros. None of these methods produce
optimum filters, however, in any normal sense.
). There is a wide variety of methods which first
fit poles and then zeros. None of these methods produce
optimum filters, however, in any normal sense.
In addition to these modifications, sometimes it is necessary to
reformulate the problem in order to achieve a different goal. For
example, in some audio applications, it is desirable to minimize the
log-magnitude frequency-response error. This is due to the way
we hear spectral distortions in many circumstances. A technique which
accomplishes this objective to the first order in the
![]() norm is
described in [428].
norm is
described in [428].
Sometimes the most important spectral structure is confined to an interval of the frequency domain. A question arises as to how this structure can be accurately modeled while obtaining a cruder fit elsewhere. The usual technique is a weighting function versus frequency. An alternative, however, is to frequency-warp the problem using a first-order conformal map. It turns out a first-order conformal map can be made to approximate very well frequency-resolution scales of human hearing such as the Bark scale or ERB scale [459]. Frequency-warping is especially valuable for providing an effective weighting function connection for filter-design methods, such as the Hankel-norm method, that are intrinsically do not offer choice of a weighted norm for the frequency-response error.
There are several methods which produce
![]() instead of
instead of
![]() directly. A fast spectral factorization technique is
useful in conjunction with methods of this category [428].
Roughly speaking, a size
directly. A fast spectral factorization technique is
useful in conjunction with methods of this category [428].
Roughly speaking, a size
![]() polynomial factorization is replaced
by an FFT and a size
polynomial factorization is replaced
by an FFT and a size
![]() system of linear equations.
system of linear equations.
Next Section:
Digital Differentiator Design
Previous Section:
Ideal Differentiator (Spring Admittance)