Ideal Differentiator (Spring Admittance)
Figure 8.1 shows a graph of the frequency response of the
ideal differentiator (spring admittance). In principle, a
digital differentiator is a filter whose frequency response
![]() optimally approximates
optimally approximates ![]() for
for ![]() between
between ![]() and
and ![]() . Similarly, a digital integrator must
match
. Similarly, a digital integrator must
match ![]() along the unit circle in the
along the unit circle in the ![]() plane. The reason
an exact match is not possible is that the ideal frequency responses
plane. The reason
an exact match is not possible is that the ideal frequency responses
![]() and
and ![]() , when wrapped along the unit circle in the
, when wrapped along the unit circle in the
![]() plane, are not ``smooth'' functions any more (see
Fig.8.1). As a result, there is no filter with a
rational transfer function (i.e., finite order) that can match the
desired frequency response exactly.
plane, are not ``smooth'' functions any more (see
Fig.8.1). As a result, there is no filter with a
rational transfer function (i.e., finite order) that can match the
desired frequency response exactly.
![\includegraphics[scale=0.9]{eps/f_ideal_diff_fr_cropped}](http://www.dsprelated.com/josimages_new/pasp/img1805.png) |
The discontinuity at ![]() alone is enough to ensure that no
finite-order digital transfer function exists with the desired
frequency response. As with bandlimited interpolation (§4.4),
it is good practice to reserve a ``guard band'' between the highest
needed frequency
alone is enough to ensure that no
finite-order digital transfer function exists with the desired
frequency response. As with bandlimited interpolation (§4.4),
it is good practice to reserve a ``guard band'' between the highest
needed frequency
![]() (such as the limit of human hearing) and half
the sampling rate
(such as the limit of human hearing) and half
the sampling rate ![]() . In the guard band
. In the guard band
![]() , digital
filters are free to smoothly vary in whatever way gives the best
performance across frequencies in the audible band
, digital
filters are free to smoothly vary in whatever way gives the best
performance across frequencies in the audible band
![]() at the
lowest cost. Figure 8.2 shows an example.
Note that, as with filters used for bandlimited
interpolation, a small increment in oversampling factor yields a much
larger decrease in filter cost (when the sampling rate is near
at the
lowest cost. Figure 8.2 shows an example.
Note that, as with filters used for bandlimited
interpolation, a small increment in oversampling factor yields a much
larger decrease in filter cost (when the sampling rate is near
![]() ).
).
In the general case of Eq.![]() (8.14) with
(8.14) with ![]() , digital filters
can be designed to implement arbitrarily accurate admittance transfer
functions by finding an optimal rational approximation to the complex
function of a single real variable
, digital filters
can be designed to implement arbitrarily accurate admittance transfer
functions by finding an optimal rational approximation to the complex
function of a single real variable ![]()
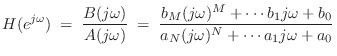
Next Section:
Digital Filter Design Overview
Previous Section:
Relation to Finite Difference Approximation



















