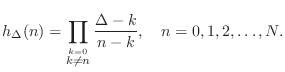Free Books    Physical Audio Signal Processing  

Explicit Lagrange Coefficient Formulas

Given a desired fractional delay of $ \Delta$ samples, the Lagrange fraction-delay impulse response can be written in closed form as

$\displaystyle h_\Delta(n) = \prod_{\stackrel{k=0}{k\neq n}} \frac{\Delta-k}{n-k}, \quad n=0,1,2,\ldots,N. \protect$ (5.7)

The following table gives specific examples for orders 1, 2, and 3:

\begin{displaymath} {\small \begin{array}{\vert\vert r\vert\vert c\vert c\vert c... ... \frac{\Delta(\Delta-1)(\Delta-2)}{6} \\ \hline \end{array}} \end{displaymath}

Note that, for $ N=1$, Lagrange interpolation reduces to linear interpolation, i.e., the interpolator impulse response is $ h = [1-\Delta,\Delta]$. Also, remember that, for order $ N$, the desired delay should be in a one-sample range centered about $ \Delta=N/2$.

Next Section:
Lagrange Interpolation Coefficient Symmetry
Previous Section:
Lagrange Interpolation Optimality