DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Lagrange Interpolation Optimality

As derived in §4.2.14, Lagrange fractional-delay filters are maximally flat in the frequency domain at dc. That is,

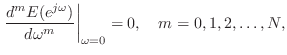
$\displaystyle \left.\frac{d^m E(e^{j\omega})}{d\omega^m}\right\vert _{\omega=0} = 0, \quad m=0,1,2,\ldots,N, $

where $ E(e^{j\omega})$ is the interpolation error expressed in the frequency domain:

$\displaystyle E(e^{j\omega})\isdefs H^\ast(e^{j\omega}) - H(e^{j\omega}), $

where $ H$ and $ H^\ast$ are defined in §4.2.2 above. This is the same optimality criterion used for the power response of (recursive) Butterworth filters in classical analog filter design [343,449]. It can also be formulated in terms of ``Pade approximation'' [373,374]. To summarize, the basic idea of maximally flat filter design is to match exactly as many leading terms as possible in the Taylor series expansion of the desired frequency response. Equivalently, we zero the maximum number of leading terms in the Taylor expansion of the frequency-response error.

Figure 4.11 compares Lagrange and optimal Chebyshev fractional-delay filter frequency responses. Optimality in the Chebyshev sense means minimizing the worst-case error over a given frequency band (in this case, $ \vert\omega\vert\in [0,0.8\pi]$). While Chebyshev optimality is often the most desirable choice, we do not have closed-form formulas for such solutions, so they must be laboriously pre-calculated, tabulated, and interpolated to produce variable-delay filtering [358].

Figure 4.11: Comparison of Lagrange and Optimal Chebyshev Fractional-Delay Filter Frequency Responses
\includegraphics[width=3.5in]{eps/lag}

Next Section:
Explicit Lagrange Coefficient Formulas
Previous Section:
Fractional Delay Filters