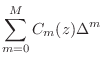Farrow Structure
Taking the z transform of Eq.![]() (4.9) yields
(4.9) yields
Since
Such a parametrization of a variable filter as a polynomial in
fixed filters ![]() is called a Farrow structure
[134,502]. When the polynomial Eq.
is called a Farrow structure
[134,502]. When the polynomial Eq.![]() (4.10) is
evaluated using Horner's rule,5.5 the efficient structure of
Fig.4.19 is obtained. Derivations of Farrow-structure
coefficients for Lagrange fractional-delay filtering are introduced in
[502, §3.3.7].
(4.10) is
evaluated using Horner's rule,5.5 the efficient structure of
Fig.4.19 is obtained. Derivations of Farrow-structure
coefficients for Lagrange fractional-delay filtering are introduced in
[502, §3.3.7].
![\includegraphics[width=\twidth]{eps/farrow}](http://www.dsprelated.com/josimages_new/pasp/img1087.png) |
As we will see in the next section, Lagrange interpolation can be
implemented exactly by the Farrow structure when ![]() . For
. For ![]() ,
approximations that do not satisfy the exact interpolation property
can be computed [148].
,
approximations that do not satisfy the exact interpolation property
can be computed [148].
Next Section:
Farrow Structure Coefficients
Previous Section:
Polynomials in the Delay








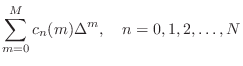
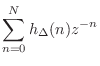
![$\displaystyle \sum_{n=0}^N \left[\sum_{m=0}^M c_n(m)\Delta^m\right]z^{-n}$](http://www.dsprelated.com/josimages_new/pasp/img1079.png)
![$\displaystyle \sum_{m=0}^M \left[\sum_{n=0}^N c_n(m) z^{-n}\right]\Delta^m$](http://www.dsprelated.com/josimages_new/pasp/img1080.png)