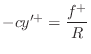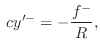Localized Velocity Excitations
Initial velocity excitations are straightforward in the DW paradigm,
but can be less intuitive in the FDTD domain. It is well known that
velocity in a displacement-wave DW simulation is determined by the
difference of the right- and left-going waves
[437]. Specifically, initial velocity waves ![]() can
be computed from from initial displacement waves
can
be computed from from initial displacement waves ![]() by spatially
differentiating
by spatially
differentiating ![]() to obtain traveling slope waves
to obtain traveling slope waves
![]() , multiplying by minus the tension
, multiplying by minus the tension ![]() to obtain force
waves, and finally dividing by the wave impedance
to obtain force
waves, and finally dividing by the wave impedance
![]() to
obtain velocity waves:
to
obtain velocity waves:
where
We can see from Eq.![]() (E.11) that such asymmetry can be caused by
unequal weighting of
(E.11) that such asymmetry can be caused by
unequal weighting of ![]() and
and
![]() . For example, the
initialization
. For example, the
initialization
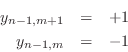
corresponds to an impulse velocity excitation at position
![]() . In this case, both interleaved grids are excited.
. In this case, both interleaved grids are excited.
Next Section:
More General Velocity Excitations
Previous Section:
Localized Displacement Excitations