More General Velocity Excitations
From Eq.![]() (E.11), it is clear that initializing any single K variable
(E.11), it is clear that initializing any single K variable
![]() corresponds to the initialization of an infinite number of W
variables
corresponds to the initialization of an infinite number of W
variables
![]() and
and
![]() . That is, a single K variable
. That is, a single K variable ![]() corresponds to only a single column of
corresponds to only a single column of
![]() for only one of the
interleaved grids. For example,
referring to Eq.
for only one of the
interleaved grids. For example,
referring to Eq.![]() (E.11),
initializing the K variable
(E.11),
initializing the K variable
![]() to -1 at time
to -1 at time ![]() (with all other
(with all other ![]() intialized to 0)
corresponds to the W-variable initialization
intialized to 0)
corresponds to the W-variable initialization
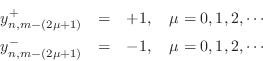
with all other W variables being initialized to zero.
In view of earlier remarks, this corresponds to an impulsive velocity
excitation on only one of the two subgrids. A schematic
depiction from ![]() to
to ![]() of the W variables at time
of the W variables at time ![]() is as
follows:
is as
follows:
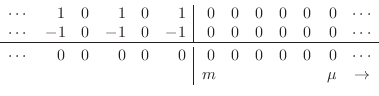 |
(E.14) |
Below the solid line is the sum of the left- and right-going traveling-wave components, i.e., the corresponding K variables at time
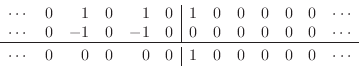 |
(E.15) |
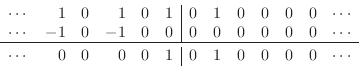 |
(E.16) |
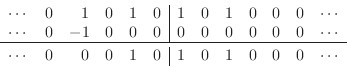 |
(E.17) |
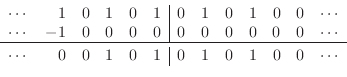 |
(E.18) |
The sequence
Due to the independent interleaved subgrids in the FDTD algorithm, it is nearly always non-physical to excite only one of them, as the above example makes clear. It is analogous to illuminating only every other pixel in a digital image. However, joint excitation of both grids may be accomplished either by exciting adjacent spatial samples at the same time, or the same spatial sample at successive times instants.
In addition to the W components being non-local, they can demand a
larger dynamic range than the K variables. For example, if the entire
semi-infinite string for ![]() is initialized with velocity
is initialized with velocity ![]() ,
the initial displacement traveling-wave components look as follows:
,
the initial displacement traveling-wave components look as follows:
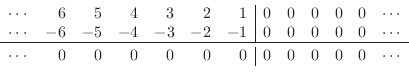 |
(E.19) |
and the variables evolve forward in time as follows:
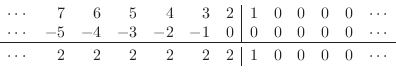 |
(E.20) |
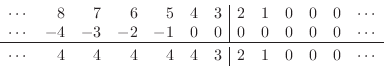 |
(E.21) |
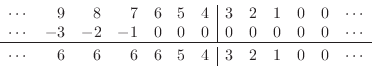 |
(E.22) |
Thus, the left semi-infinite string moves upward at a constant velocity of 2, while a ramp spreads out to the left and right of position
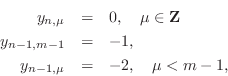
where ![]() denotes the set of all integers.
While the FDTD excitation is also not local, of course, it is
bounded for all
denotes the set of all integers.
While the FDTD excitation is also not local, of course, it is
bounded for all ![]() .
.
Since the traveling-wave components of initial velocity excitations are generally non-local in a displacement-based simulation, as illustrated in the preceding examples, it is often preferable to use velocity waves (or force waves) in the first place [447].
Another reason to prefer force or velocity waves is that displacement
inputs are inherently impulsive. To see why this is so, consider that
any physically correct driving input must effectively exert some
finite force on the string, and this force is free to change
arbitrarily over time. The ``equivalent circuit'' of the infinitely
long string at the driving point is a ``dashpot'' having real,
positive resistance
![]() . The applied force
. The applied force ![]() can be
divided by
can be
divided by ![]() to obtain the velocity
to obtain the velocity ![]() of the string driving
point, and this velocity is free to vary arbitrarily over time,
proportional to the applied force. However, this velocity must be
time-integrated to obtain a displacement
of the string driving
point, and this velocity is free to vary arbitrarily over time,
proportional to the applied force. However, this velocity must be
time-integrated to obtain a displacement ![]() . Therefore,
there can be no instantaneous displacement response to a finite
driving force. In other words, any instantaneous effect of an input
driving signal on an output displacement sample is non-physical except
in the case of a massless system. Infinite force is required to move
the string instantaneously. In sampled displacement simulations, we
must interpret displacement changes as resulting from time-integration
over a sampling period. As the sampling rate increases, any
physically meaningful displacement driving signal must converge to
zero.
. Therefore,
there can be no instantaneous displacement response to a finite
driving force. In other words, any instantaneous effect of an input
driving signal on an output displacement sample is non-physical except
in the case of a massless system. Infinite force is required to move
the string instantaneously. In sampled displacement simulations, we
must interpret displacement changes as resulting from time-integration
over a sampling period. As the sampling rate increases, any
physically meaningful displacement driving signal must converge to
zero.
Next Section:
Additive Inputs
Previous Section:
Localized Velocity Excitations



















