DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Mass Moment of Inertia

The mass moment of inertia $ I$ (or simply moment of inertia), plays the role of mass in rotational dynamics, as we saw in Eq.$ \,$(B.7) above.

The mass moment of inertia of a rigid body, relative to a given axis of rotation, is given by a weighted sum over its mass, with each mass-point weighted by the square of its distance from the rotation axis. Compare this with the center of mass (§B.4.1) in which each mass-point is weighted by its vector location in space (and divided by the total mass).

Equation (B.8) above gives the moment of inertia for a single point-mass $ m$ rotating a distance $ R$ from the axis to be $ I=mR^2$. Therefore, for a rigid collection of point-masses $ m_i$, $ i=1,\ldots,N$,B.14 the moment of inertia about a given axis of rotation is obtained by adding the component moments of inertia:

$\displaystyle I = m_1 R_1^2 + m_2 R_2^2 + \cdots + m_N R_N^2, \protect$ (B.9)

where $ R_i$ is the distance from the axis of rotation to the $ i$th mass.

For a continuous mass distribution, the moment of inertia is given by integrating the contribution of each differential mass element:

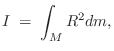$\displaystyle I \eqsp \int_M R^2 dm,$ (B.10)

where $ R$ is the distance from the axis of rotation to the mass element $ dm$. In terms of the density $ \rho(\underline{x})$ of a continuous mass distribution, we can write

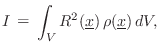
$\displaystyle I \,\mathrel{\mathop=}\,\int_V R^2(\underline{x})\,\rho(\underline{x})\,dV, $

where $ \rho(\underline{x})$ denotes the mass density (kg/m$ \null^3$) at the point $ \underline{x}$, and $ dV=dx\,dy\,dz$ denotes a differential volume element located at $ \underline{x}\in{\bf R}^3$.

Circular Disk Rotating in Its Own Plane

For example, the moment of inertia for a uniform circular disk of total mass $ M$ and radius $ R$, rotating in its own plane about a rotation axis piercing its center, is given by

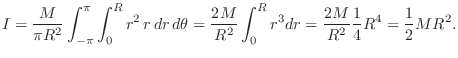
$\displaystyle I = \frac{M}{\pi R^2}\int_{-\pi}^\pi \int_0^R r^2\, r\,dr\,d\thet... ...c{2M}{R^2}\int_0^R r^3 dr = \frac{2M}{R^2}\frac{1}{4} R^4 = \frac{1}{2} M R^2. $

Circular Disk Rotating About Its Diameter

The moment of inertia for the same circular disk rotating about an axis in the plane of the disk, passing through its center, is given by

$\displaystyle I = \frac{M}{\pi R^2}\cdot 4\int_0^{\pi/2} \int_0^R [r\cos(\theta)]^2\, r\,dr\,d\theta = \frac{1}{4}MR^2 $

Thus, the uniform disk's moment of inertia in its own plane is twice that about its diameter.

Next Section:
Perpendicular Axis Theorem
Previous Section:
Rotational Kinetic Energy