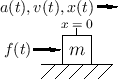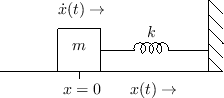Ordinary Differential Equations
(ODEs) typically result
directly from Newton's laws of motion, restated here as
follows:
This is a second-order ODE relating the force
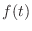
on a mass

at
time

to the second time-derivative of its position

,
i.e.,
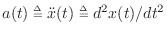
. A physical diagram
is shown in Fig.
1.1. From this ODE we can see that a
constant applied force

results in a constant acceleration
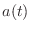
, a linearly increasing
velocity
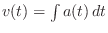
, and
quadratically increasing position

. The initial
position

and velocity
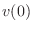
of the mass comprise the
initial state of mass, and serve as the
boundary
conditions for the ODE. The boundary conditions must be known in
order to determine the two constants of integration needed when
computing

for
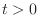
.
Figure 1.1:
Physical diagram of an external force driving a mass
sliding on a frictionless surface.
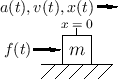 |
If the applied force 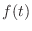 is due to a spring with spring-constant
is due to a spring with spring-constant
 , then we may write the ODE as
, then we may write the ODE as
This case is diagrammed in Fig.
1.2.
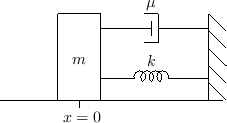
If the mass is sliding with friction, then a simple ODE model
is given by
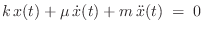
(Spring + Friction + Inertial Forces = 0)
as depicted in Fig.
1.3.
We will use such ODEs to model mass, spring, and dashpot2.6 elements
in Chapter 7.
Next Section: PDEsPrevious Section: Formulations
![]() is due to a spring with spring-constant
is due to a spring with spring-constant
![]() , then we may write the ODE as
, then we may write the ODE as