DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Plane Waves in Air

Figure B.9 shows a 2D $ xy$ cross-section of a snapshot (in time) of the sinusoidal plane wave

$\displaystyle p(x,y,z) = p_0 + \cos(k_x x + k_y y) $

for $ k_x = 2\pi 5$ and $ k_y=2\pi 5/2$, with $ x$ and $ y$ in the range $ [0,1)$.

Figure: Gray-scale density plot of the $ xy$ cross-section of a sinusoidal plane wave $ p(t,\underline{x}) = \cos\left(\omega t - \underline{k}^T\underline{x}\right)$, at $ t=0$ with vector wavenumber $ \underline{k}^T=[10\pi, 5\pi, 0]$.
\includegraphics[width=\twidth]{eps/planewave}

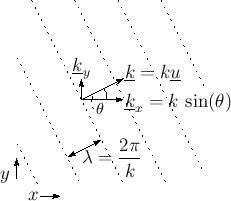
Figure B.10 depicts a more mathematical schematic of a sinusoidal plane wave traveling toward the upper-right of the figure. The dotted lines indicate the crests (peak amplitude location) along the wave.

Figure: Wave crests of the sinusoidal traveling plane wave $ p(t,\underline{x}) = \cos\left(\omega t - \underline{k}^T\underline{x}\right)$, for some fixed time $ t$ and $ \underline{x}$ in the $ (x,y,0)$ plane.
\includegraphics{eps/planewaveangle}

The direction of travel and spatial frequency are indicated by the vector wavenumber $ \underline{k}$, as discussed in in the following section.

Next Section:
Vector Wavenumber
Previous Section:
Air Absorption