DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Prime Power Delay-Line Lengths

When the delay-line lengths need to be varied in real time, or interactively in a GUI, it is convenient to choose each delay-line length $ \hat{M}_i$ as an integer power of a distinct prime number $ p_i$ [457]:

$\displaystyle \hat{M}_i \isdefs p_i^{m_i} $

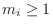
where we call $ m_i\ge 1$ the ``multiplicity'' of the prime $ p_i$. With this choice, the delay-line lengths are always coprime (no factors in common other than $ 1$), and yet we can lengthen or shorten each delay line individually (by factors of $ p_i$) without affecting the mutually prime property.

Suppose we are initially given desired delay-line lengths $ M_i$ arranged in ascending order so that

$\displaystyle M_1 < M_2 < \cdots < M_N. $

Then good prime-power approximations $ \hat{M}_i$ can be expected using the prime numbers in their natural order:

$\displaystyle p_i \in \{2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,\ldots\} $

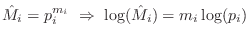
Since $ \hat{M}_i=p_i^{m_i} \,\,\Rightarrow\,\,\log(\hat{M}_i) = m_i \log(p_i)$ (for any logarithmic base), an optimal (in some sense) choice of prime multiplicity $ m_i$ is

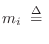
$\displaystyle m_i \isdefs$   round$\displaystyle \left[\frac{\log(M_i)}{\log(p_i)}\right] \isdefs \left\lfloor 0.5 + \frac{\log(M_i)}{\log(p_i)}\right\rfloor. $

where $ M_i$ is the desired length in samples. That is, $ m_i$ can be simply obtained by rounding $ \log(M_i)/\log(p_i)$ to the nearest integer (max 1). The prime-power delay-line length approximation is then of course

$\displaystyle \hat{M}_i \isdefs p_i^{m_i}, $

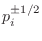
and the multiplicative approximation error is bounded by $ p_i^{\pm1/2}$ (when $ M_i\ge\sqrt{p_i}$).

This prime-power length scheme is used to keep 16 delay lines both variable and mutually prime in Faust's reverb_designer.dsp programming example (via the function prime_power_delays in effect.lib).

Next Section:
Conformal Map Interpretation of Damping Substitution
Previous Section:
Mode Density Requirement