DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Mode Density Requirement

A guide for the sum of the delay-line lengths is the desired mode density. The sum of delay-line lengths $ M_i$ in a lossless FDN is simply the order of the system $ M$:

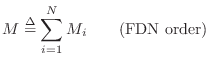
$\displaystyle M \isdef \sum_{i=1}^N M_i\qquad\hbox{(FDN order)} $

The order increases slightly when lowpass filters are introduced after the delay lines to achieve a specific reverberation time at low and high frequencies (as described in the next subsection).

Since the order of a system equals the number of poles, we have that $ M$ is the number of poles on the unit circle in the lossless prototype. If the modes were uniformly distributed, the mode density would be $ M/f_s=MT$ modes per Hz. Schroeder [417] suggests that, for a reverberation time of 1 second, a mode density of 0.15 modes per Hz is adequate. Since the mode widths are inversely proportional to reverberation time, the mode density for a reverberation time of 2 seconds should be 0.3 modes per Hz, etc. In summary, for a sufficient mode density in the frequency domain, Schroeder's formula is

$\displaystyle M \geq 0.15 t_{60}f_s $

For a sampling rate of 50 kHz and a reverberation time ($ t_{60}$) equal to 1 second, we obtain $ M\geq 7500$.

Next Section:
Prime Power Delay-Line Lengths
Previous Section:
Mean Free Path