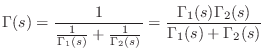Series Combination of One-Ports

Figure 7.6 shows the series combination of two one-ports.

**Figure 7.6:** Two one-port networks combined in series. The impedance of the series combination is .
$\includegraphics[scale=0.9]{eps/lseries}$

Impedances add in series, so the aggregate impedance is , and the admittance is

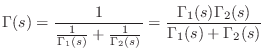
$\displaystyle \Gamma(s) = \frac{1}{\frac{1}{\Gamma_1(s)} + \frac{1}{\Gamma_2(s)}} = \frac{\Gamma_1(s) \Gamma_2(s) }{\Gamma_1(s) + \Gamma_2(s)}$

The latter expression is the handy product-over-sum rule for combining admittances in series.

Next Section:
Mass-Spring-Wall System
Previous Section:
Ideal Spring

Sign in