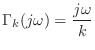DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Ideal Spring

Figure 7.4 depicts the ideal spring.

Figure 7.4: The ideal spring characterized by $ f(t) = k x(t)$.
\includegraphics[width=3in]{eps/lspring}

From Hooke's law, we have that the applied force is proportional to the displacement of the spring:

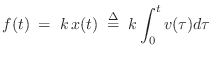
$\displaystyle f(t) \eqsp k\, x(t) \isdefs k \int_0^t v(\tau)d\tau $

where it is assumed that $ x(0) = 0$. The spring constant $ k$ is sometimes called the stiffness of the spring. Taking the Laplace transform gives

$\displaystyle F(s) = k V(s)/s $

so that the impedance of a spring is

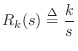
$\displaystyle R_k(s) \isdef \frac{k}{s} $

and the admittance is

$\displaystyle \Gamma_k(s) \isdef \frac{s}{k} $

This is the transfer function of a differentiator. We can say that the ideal spring differentiates the applied force (divided by $ k$) to produce the output velocity.

The frequency response of the ideal spring, given the applied force as input and resulting velocity as output, is

$\displaystyle \Gamma_k(j\omega) = \frac{j\omega}{k} $

In this case, the amplitude response grows $ +6$ dB per octave, and the phase shift is $ +\pi /2$ radians for all $ \omega $. Clearly, there is no such thing as an ideal spring which can produce arbitrarily large gain as frequency goes to infinity; there is always some mass in a real spring.

We call $ v(t)$ the compression velocity of the spring. In more complicated configurations, the compression velocity is defined as the difference between the velocity of the two spring endpoints, with positive velocity corresponding to spring compression.

In circuit theory, the element analogous to the spring is the capacitor, characterized by $ i(t) = C dv/dt$, or $ I(s) = Cs V(s)$. In an equivalent analog circuit, we can use the value $ C = 1/k$. The inverse $ 1/k$ of the spring stiffness is sometimes called the compliance of the spring.

Don't forget that the definition of impedance requires zero initial conditions for elements with ``memory'' (masses and springs). This means we can only use impedance descriptions for steady state analysis. For a complete analysis of a particular system, including the transient response, we must go back to full scale Laplace transform analysis.

Next Section:
Series Combination of One-Ports
Previous Section:
Ideal Mass