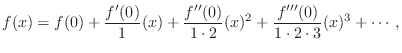Series Expansions
Any ``smooth'' function
can be expanded as a Taylor series expansion:
where ``smooth'' means that derivatives of all orders must exist over the range of validity. Derivatives of all orders are obviously needed at
by the above expansion, and for the expansion to be valid
everywhere, the function must be smooth for all 
.
Next Section:
Arctangent Series Expansion
Previous Section:
Cubic Soft Clipper
