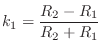Signal Scattering
The digital waveguide was introduced in §2.4. A basic fact from acoustics is that traveling waves only happen in a uniform medium. For a medium to be uniform, its wave impedance3.17must be constant. When a traveling wave encounters a change in the wave impedance, it will reflect, at least partially. If the reflection is not total, it will also partially transmit into the new impedance. This is called scattering of the traveling wave.
Let ![]() denote the constant impedance in some waveguide, such as a
stretched steel string or acoustic bore. Then signal scattering is
caused by a change in wave impedance from
denote the constant impedance in some waveguide, such as a
stretched steel string or acoustic bore. Then signal scattering is
caused by a change in wave impedance from ![]() to
to ![]() . We can
depict the partial reflection and transmission as shown in
Fig.2.33.
. We can
depict the partial reflection and transmission as shown in
Fig.2.33.
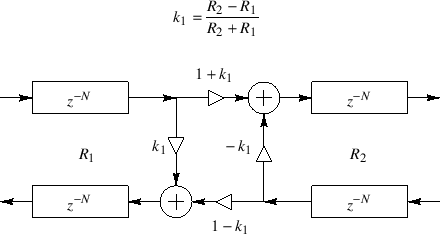
The computation of reflection and transmission in both directions, as shown in Fig.2.33 is called a scattering junction.
As derived in Appendix C, for force or pressure waves, the
reflection coefficient ![]() is given by
is given by
That is, the coefficient of reflection for a traveling pressure wave leaving impedance
For velocity traveling waves, the reflection coefficient is
just the negative of that for force/pressure waves, or ![]() (see
Appendix C).
(see
Appendix C).
Signal scattering is lossless, i.e., wave energy is neither
created nor destroyed. An implication of this is that the
transmission coefficient
for a traveling pressure wave leaving impedance ![]() and entering
impedance
and entering
impedance ![]() is given by
is given by
Next Section:
Digital Waveguide Networks
Previous Section:
Gerzon Nested MIMO Allpass