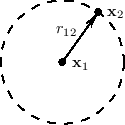Spherical Waves from a Point Source
Acoustic theory tells us that a point source produces a spherical wave in an ideal isotropic (uniform) medium such as air. Furthermore, the sound from any radiating surface can be computed as the sum of spherical wave contributions from each point on the surface (including any relevant reflections). The Huygens-Fresnel principle explains wave propagation itself as the superposition of spherical waves generated at each point along a wavefront (see, e.g., [349, p. 175]). Thus, all linear acoustic wave propagation can be seen as a superposition of spherical traveling waves.
To a good first approximation, wave energy is conserved as it
propagates through the air. In a spherical pressure wave of radius
![]() , the energy of the wavefront is spread out over the spherical
surface area
, the energy of the wavefront is spread out over the spherical
surface area ![]() . Therefore, the energy per unit area of an
expanding spherical pressure wave decreases as
. Therefore, the energy per unit area of an
expanding spherical pressure wave decreases as ![]() . This is
called spherical spreading loss. It is also an example of an
inverse square law which is found repeatedly in the physics of
conserved quantities in three-dimensional space. Since energy is
proportional to amplitude squared, an inverse square law for energy
translates to a
. This is
called spherical spreading loss. It is also an example of an
inverse square law which is found repeatedly in the physics of
conserved quantities in three-dimensional space. Since energy is
proportional to amplitude squared, an inverse square law for energy
translates to a ![]() decay law for amplitude.
decay law for amplitude.
The sound-pressure amplitude of a traveling wave is proportional to
the square-root of its energy per unit area. Therefore, in a
spherical traveling wave, acoustic amplitude is proportional to ![]() ,
where
,
where ![]() is the radius of the sphere. In terms of Cartesian
coordinates, the amplitude
is the radius of the sphere. In terms of Cartesian
coordinates, the amplitude
![]() at the point
at the point
![]() due to a point source located at
due to a point source located at
![]() is given by
is given by
In summary, every point of a radiating sound source emits spherical
traveling waves in all directions which decay as ![]() , where
, where ![]() is
the distance from the source. The amplitude-decay by
is
the distance from the source. The amplitude-decay by ![]() can be
considered a consequence of energy conservation for propagating waves.
(The energy spreads out over the surface of an expanding sphere.) We
often visualize such waves as ``rays'' emanating from the source, and
we can simulate them as a delay line along with a
can be
considered a consequence of energy conservation for propagating waves.
(The energy spreads out over the surface of an expanding sphere.) We
often visualize such waves as ``rays'' emanating from the source, and
we can simulate them as a delay line along with a ![]() scaling
coefficient (see Fig.2.7). In contrast, since
plane waves propagate with no decay at all, each ``ray'' can be
considered lossless, and the simulation involves only a delay line
with no scale factor, as shown in Fig.2.1 on page
scaling
coefficient (see Fig.2.7). In contrast, since
plane waves propagate with no decay at all, each ``ray'' can be
considered lossless, and the simulation involves only a delay line
with no scale factor, as shown in Fig.2.1 on page ![]() .
.
Next Section:
Reflection of Spherical or Plane Waves
Previous Section:
Converting Propagation Distance to Delay Length