Converting Propagation Distance to Delay Length

We may regard the delay-line memory itself as the fixed ``air'' which propagates sound samples at a fixed speed ( meters per second at degrees Celsius and 1 atmosphere). The input signal can be associated with a sound source, and the output signal (see Fig.2.1 on page ) can be associated with the listening point. If the listening point is meters away from the source, then the delay line length needs to be

where denotes the discrete-time sampling interval. In other words, the number of samples delay is the propagation distance divided by , the distance sound propagates in one sampling interval. In practice, rounding to the nearest integer causes no audible difference, unless the echo time is so short that the system is not really perceived as an echo (we'll learn about ``comb filters'' in §2.6 below).

---

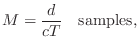
Next Section:
Spherical Waves from a Point Source
Previous Section:
Dispersive Traveling Waves

Sign in