Summary of Flanging

In view of the above, we may define a flanger in general as any filter which modulates the frequencies of a set of uniformly spaced notches and/or peaks in the frequency response. The main parameters are

• Depth -- controlling notch depth
• Speed -- speed of notch movement
• Phase -- switch to subtract instead of adding the direct signal with the delayed signal

• Average Delay
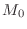
• Excursion or Sweep -- amount by which the delay-line grows or shrinks
• Feedback or Regeneration 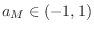-- feedback coefficient from output to input

Note that flanging provides only uniformly spaced notches. This can be considered non-ideal for several reasons. First, the ear processes sound over a frequency scale that is more nearly logarithmic than linear [459]. Therefore, exponentially spaced notches (uniformly spaced on a log frequency scale) should sound more uniform perceptually. Secondly, the uniform peaks and notches of the flanger can impose a discernible ``resonant pitch'' on the program material, giving the impression of being inside a resonant tube. Third, when (inverted flanging), it is possible for a periodic tone to be completely annihilated by harmonically spaced notches if the harmonics of the tone are unlucky enough to land exactly on a subset of the harmonic notches. In practice, exact alignment is unlikely; however, the signal loudness can be modulated to a possibly undesirable degree as the notches move through alignment with the signal spectrum. For this reason, flangers are best used with noise-like or inharmonic sounds. For harmonic signals, it makes sense to consider methods for creating non-uniform moving notches.

A Faust software implementation of flanging may be found in the file effect.lib within the Faust distribution [154,170]. The Faust programming example phaser_flanger.dsp may be run to hear the effect on a test signal and experiment with its parameters in real time.

Sign in