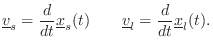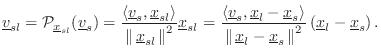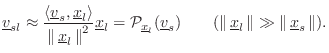DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Vector Formulation

Denote the sound-source velocity by $ \underline{v}_s(t)$ where $ t$ is time. Similarly, let $ \underline{v}_l(t)$ denote the velocity of the listener, if any. The position of source and listener are denoted $ \underline{x}_s(t)$ and $ \underline{x}_l(t)$, respectively, where $ \underline{x}\isdef (x_1,x_2,x_3)^T$ is 3D position. We have velocity related to position by

$\displaystyle \underline{v}_s= \frac{d}{dt}\underline{x}_s(t) \qquad \underline{v}_l= \frac{d}{dt}\underline{x}_l(t). \protect$ (6.3)

Consider a Fourier component of the source at frequency $ \omega_s $. We wish to know how this frequency is shifted to $ \omega_l $ at the listener due to the Doppler effect.

The Doppler effect depends only on velocity components along the line connecting the source and listener [349, p. 453]. We may therefore orthogonally project the source and listener velocities onto the vector $ \underline{x}_{sl}=\underline{x}_l-\underline{x}_s$ pointing from the source to the listener. (See Fig.5.8 for a specific example.)

The orthogonal projection of a vector $ \underline{x}$ onto a vector $ {\underline{y}}$ is given by [451]

$\displaystyle {\cal P}_{\underline{y}}(\underline{x}) = \frac{\left<\underline{... ...derline{x}^T{\underline{y}}}{{\underline{y}}^T{\underline{y}}}{\underline{y}}. $

Therefore, we can write the projected source velocity as

$\displaystyle \underline{v}_{sl}= {\cal P}_{\underline{x}_{sl}}(\underline{v}_s... ...line{x}_s\,\right\Vert^2}\left(\underline{x}_l-\underline{x}_s\right). \protect$ (6.4)

In the far field (listener far away), Eq.$ \,$(5.4) reduces to

$\displaystyle \underline{v}_{sl} \approx \frac{\left<\underline{v}_s,\underline... ...derline{x}_l\,\right\Vert\gg\left\Vert\,\underline{x}_s\,\right\Vert). \protect$ (6.5)

Next Section:
Doppler Simulation via Delay Lines
Previous Section:
Summary of Flanging