Thiran Allpass Interpolators

Free Books Physical Audio Signal Processing

Given a desired delay $\Delta = N+\delta$ samples, an order allpass filter

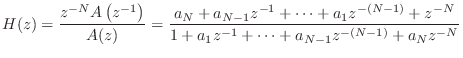
$\displaystyle H(z) = \frac{z^{-N}A\left(z^{-1}\right)}{A(z)} = \frac{a_N + a_{N... ...^{-(N-1)} + z^{-N}}{1 + a_1 z^{-1} + \cdots + a_{N-1} z^{-(N-1)} + a_N z^{-N}}$

can be designed having maximally flat group delay equal to $\Delta$ at dc using the formula

$\displaystyle a_k=(-1)^k\left(\begin{array}{c} N \\ [2pt] k \end{array}\right)\prod_{n=0}^N\frac{\Delta-N+n}{\Delta-N+k+n}, \; k=0,1,2,\ldots,N$

where

$\displaystyle \left(\begin{array}{c} N \\ [2pt] k \end{array}\right) = \frac{N!}{k!(N-k)!}$

denotes the

th binomial coefficient. Note, incidentally, that a lowpass filter having maximally flat group-delay at dc is called a Bessel filter [362, pp. 228-230].

without further scaling
For sufficiently large $\Delta$ , stability is guaranteed
Rule of thumb: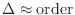 $\Delta \approx \hbox{order}$
It can be shown that the mean group delay of any stable th-order allpass filter is samples [449].^5.7
Only known closed-form case for allpass interpolators of arbitrary order
Effective for delay-line interpolation needed for tuning since pitch perception is most acute at low frequencies.
Since Thiran allpass filters have maximally flat group-delay at dc, like Lagrange FIR interpolation filters, they can be considered the recursive extension of Lagrange interpolation.

Thiran Allpass Interpolation in Matlab

function [A,B] = thiran(D,N)
%  [A,B] = thiran(D,N)
%  returns the order N Thiran allpass interpolation filter
%  for delay D (samples).

A = zeros(1,N+1);
for k=0:N
    Ak = 1;
    for n=0:N
        Ak = Ak * (D-N+n)/(D-N+k+n);
    end
    A(k+1) = (-1)^k * nchoosek(N,k) * Ak;
end

B = A(N+1:-1:1);

Group Delays of Thiran Allpass Interpolators

Figure shows a family of group-delay curves for Thiran allpass interpolators, for orders 1, 2, 3, 5, 10, and 20. The desired group delay was equal to the order plus 0.3 samples (which is in the ``easy zone'' for an allpass interpolator).

**Figure 4.20:**
$\includegraphics[width=\twidth]{eps/thirangdC}$

Next Section:
Windowed Sinc Interpolation
Previous Section:
Lagrange Interpolation