DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Traveling-Wave Partial Derivatives

Because we have defined our traveling-wave components $ y_r(t-x/c)$ and $ y_l(t+x/c)$ as having arguments in units of time, the partial derivatives with respect to time $ t$ are identical to simple derivatives of these functions. Let $ {\dot y}_r$ and $ {\dot y}_l$ denote the (partial) derivatives with respect to time of $ y_r$ and $ y_l$, respectively. In contrast, the partial derivatives with respect to $ x$ are

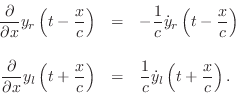
\begin{eqnarray*} \frac{\partial}{\partial x} y_r\left(t-\frac{x}{c}\right) &=&... ...c}\right) &=& \frac{1}{c}{\dot y}_l\left(t+ \frac{x}{c}\right). \end{eqnarray*}

Denoting the spatial partial derivatives by $ y'_r$ and $ y'_l$, respectively, we can write more succinctly

\begin{eqnarray*} y'_r&=& -\frac{1}{c}{\dot y}_r\\ [5pt] y'_l&=& \frac{1}{c}{\dot y}_l, \end{eqnarray*}

where this argument-free notation assumes the same $ t$ and $ x$ for all terms in each equation, and the subscript $ l$ or $ r$ determines whether the omitted argument is $ t + x/c$ or $ t - x/c$.

Now we can see that the second partial derivatives in $ x$ are

\begin{eqnarray*} y''_r&=& \left(-\frac{1}{c}\right)^2 {\ddot y}_r= \frac{1}{c^2... ...eft(\frac{1}{c}\right)^2 {\ddot y}_l= \frac{1}{c^2} {\ddot y}_l. \end{eqnarray*}

These relations, together with the fact that partial differention is a linear operator, establish that

$\displaystyle y(t,x) = y_r\left(t-\frac{x}{c}\right) + y_l\left(t+\frac{x}{c}\right). \protect$

obeys the ideal wave equation $ {\ddot y}= c^2y''$ for all twice-differentiable functions $ y_r$ and $ y_l$.

Next Section:
Use of the Chain Rule
Previous Section:
FDA of the Ideal String