Free Books
   Free Books    Physical Audio Signal Processing  

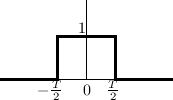
Triangular Pulse as Convolution of Two Rectangular Pulses

The 2-sample wide triangular pulse $ h_l(t)$ (Eq.$ \,$(4.4)) can be expressed as a convolution of the one-sample rectangular pulse with itself.

Figure 4.8: The width $ T$ rectangular pulse.
\includegraphics{eps/rectpulse}
The one-sample rectangular pulse is shown in Fig.4.8 and may be defined analytically as

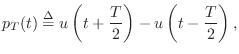
$\displaystyle p_T(t) \isdef u\left(t+\frac{T}{2}\right) - u\left(t-\frac{T}{2}\right), $

where $ u(t)$ is the Heaviside unit step function:

$\displaystyle u(t) \isdef \left\{\begin{array}{ll} 1, & t\geq 0 \\ [5pt] 0, & t<0 \\ \end{array}\right.. $

Convolving $ p_T(t)$ with itself produces the two-sample triangular pulse $ h_l(t)$:

$\displaystyle h_l(t) = (p_T\ast p_T)(t) \isdef \int_{-\infty}^{\infty} p_T(\tau)p_T(t-\tau)d\tau $

While the result can be verified algebraically by substituting $ u(t+T/2)-u(t-T/2)$ for $ p_T(t)$, it seen more quickly via graphical convolution.
Next Section:
Linear Interpolation Frequency Response
Previous Section:
Frequency Response of Linear Interpolation