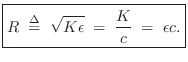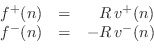Wave Impedance
A concept of high practical utility is that of wave impedance, defined for vibrating strings as force divided by velocity. As derived in §C.7.2, the relevant force quantity in this case is minus the string tension times the string slope:
| (7.4) |
Physically, this can be regarded as the transverse force acting to the right on the string in the vertical direction. (Only transverse vibration is being considered.) In other words, the vertical component of a negative string slope pulls ``up'' on the segment of string to the right, and ``up'' is the positive direction for displacement, velocity, and now force. The traveling-wave decomposition of the force into force waves is thus given by (see §C.7.2 for a more detailed derivation)7.2

where we have defined the new notation
![]() for transverse velocity, and
for transverse velocity, and
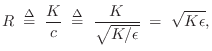
The wave impedance simply relates force and velocity traveling waves:
These relations may be called Ohm's law for traveling waves. Thus, in a traveling wave, force is always in phase with velocity (considering the minus sign in the left-going case to be associated with the direction of travel rather than a
The results of this section are derived in more detail in
Appendix C. However, all we need in practice for now are the
important Ohm's law relations for traveling-wave components given in
Eq.![]() (6.6).
(6.6).
Next Section:
Velocity Waves at a Rigid Termination
Previous Section:
Sampled Traveling-Wave Solution