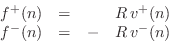Using the above identities, we have that the force distribution along
the string is given in terms of velocity waves by
![$\displaystyle f(t,x) = \frac{K}{c} \left[{\dot y}_r(t-x/c) - {\dot y}_l(t+x/c) \right], \protect$](http://www.dsprelated.com/josimages_new/pasp/img3483.png) |
(C.44) |
where
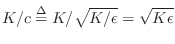
. This is a fundamental
quantity known as the
wave impedance of the string (also called
the
characteristic impedance), denoted as
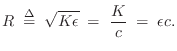 |
(C.45) |
The
wave impedance can be seen as the geometric mean of the two
resistances to
displacement: tension (
spring force) and
mass (
inertial
force).
The digitized traveling force-wave components become
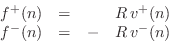 |
(C.46) |
which gives us that the right-going force wave equals the wave
impedance times the right-going velocity wave, and the left-going
force wave equals
minus the wave impedance times the left-going velocity wave.
C.4Thus, in a
traveling wave, force is always
in phase with
velocity (considering the minus sign in the left-going case to be
associated with the direction of travel rather than a
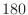
degrees
phase shift between force and velocity). Note also that if the
left-going force wave were defined as the string force acting to the
left, the minus sign would disappear. The fundamental relation
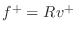
is sometimes referred to as the mechanical counterpart of
Ohm's law for traveling waves, and

in c.g.s. units
can be called
acoustical ohms [
261].
In the case of the acoustic tube [317,297], we have the
analogous relations
 |
(C.47) |
where
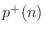
is the right-going traveling
longitudinal pressure
wave component,

is the left-going
pressure wave, and
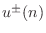
are the left and right-going
volume velocity waves. In the acoustic
tube context, the wave impedance is given by
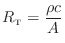 (Acoustic Tubes) (Acoustic Tubes) |
(C.48) |
where

is the mass per unit volume of air,

is
sound speed in
air, and

is the
cross-sectional area of the tube.
Note that if we had chosen
particle velocity rather than volume
velocity, the wave impedance would be
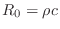
instead, the wave
impedance in open air. Particle velocity is appropriate in open air,
while volume velocity is the conserved quantity in acoustic tubes or
``ducts'' of varying cross-sectional area.
Next Section: State ConversionsPrevious Section: Force Waves
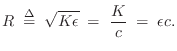









![$\displaystyle f(t,x) = \frac{K}{c} \left[{\dot y}_r(t-x/c) - {\dot y}_l(t+x/c) \right], \protect$](http://www.dsprelated.com/josimages_new/pasp/img3483.png)