State Conversions
In §C.3.6, an arbitrary string state was converted to
traveling displacement-wave components to show that the traveling-wave
representation is complete, i.e., that any physical string state can be
expressed as a pair of traveling-wave components. In this section, we
revisit this topic using force and velocity waves.
By definition of the traveling-wave decomposition, we have
Using Eq. (C.46), we can eliminate
(C.46), we can eliminate
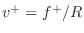 and
and
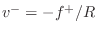 ,
giving, in matrix form,
,
giving, in matrix form,
Thus, the string state (in terms of force and velocity) is expressed
as a
linear transformation of the traveling
force-wave components. Using
the
Ohm's law relations to eliminate instead
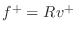
and
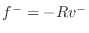
,
we obtain
To convert an arbitrary initial string state
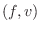
to either a
traveling force-wave or velocity-wave simulation, we simply must be
able to
invert the appropriate two-by-two matrix above. That
is, the matrix must be
nonsingular. Requiring both
determinants to be nonzero yields the condition
That is, the
wave impedance must be a positive, finite number. This
restriction makes good physical sense because one cannot
propagate a
finite-energy wave in either a zero or infinite wave
impedance.
Carrying out the inversion to obtain force waves
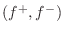 from
from
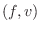 yields
yields
Similarly, velocity waves
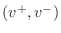
are prepared from
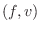
according to
Next Section: Power WavesPrevious Section: Wave Impedance![]() (C.46), we can eliminate
(C.46), we can eliminate
![]() and
and
![]() ,
giving, in matrix form,
,
giving, in matrix form,
![$\displaystyle \left[\begin{array}{c} f \\ [2pt] v \end{array}\right] = \left[\b...
...ay}\right]
\left[\begin{array}{c} f^{{+}} \\ [2pt] f^{{-}} \end{array}\right].
$](http://www.dsprelated.com/josimages_new/pasp/img3492.png)
![$\displaystyle \left[\begin{array}{c} f \\ [2pt] v \end{array}\right] = \left[\b...
...d{array}\right]\left[\begin{array}{c} v^{+} \\ [2pt] v^{-} \end{array}\right].
$](http://www.dsprelated.com/josimages_new/pasp/img3494.png)
![]() from
from
![]() yields
yields
![$\displaystyle \left[\begin{array}{c} f^{{+}} \\ [2pt] f^{{-}} \end{array}\right...
...ft[\begin{array}{c} \frac{f+Rv}{2} \\ [2pt] \frac{f-Rv}{2} \end{array}\right].
$](http://www.dsprelated.com/josimages_new/pasp/img3498.png)
![$\displaystyle \left[\begin{array}{c} v^{+} \\ [2pt] v^{-} \end{array}\right] = ...
...[\begin{array}{c} \frac{v+f/R}{2} \\ [2pt] \frac{v-f/R}{2} \end{array}\right].
$](http://www.dsprelated.com/josimages_new/pasp/img3500.png)



















