DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Wave Momentum

The physical forward momentum carried by a transverse wave along a string is conveyed by a secondary longitudinal wave [391].

A less simplified wave equation which supports longitudinal wave momentum is given by [391, Eqns. 38ab]

$\displaystyle \epsilon {\ddot \xi}$ $\displaystyle =$ $\displaystyle \left(SY+K\right) \xi^{\prime\prime} + SY\eta^\prime\eta^{\prime\prime}$ (B.40)
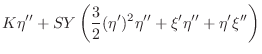$\displaystyle \epsilon {\ddot \eta}$ $\displaystyle =$ $\displaystyle K \eta^{\prime\prime} + SY\left(\frac{3}{2}(\eta^\prime)^2\eta^{\... ...rime} +\xi^{\prime}\eta^{\prime\prime} + \eta^{\prime}\xi^{\prime\prime}\right)$ (B.41)
  $\displaystyle \approx$ $\displaystyle K\eta^{\prime\prime},$ (B.42)

where $ \xi$ and $ \eta$ denote longitudinal and transverse displacement, respectively, and the commonly used ``dot'' and ``prime'' notation for partial derivatives has been introduced, e.g.,
$\displaystyle {\dot \xi}$ $\displaystyle \isdef$ $\displaystyle \frac{\partial \xi}{\partial t}$ (B.43)
$\displaystyle {\xi^{\prime}}$ $\displaystyle \isdef$ $\displaystyle \frac{\partial \xi}{\partial x}.$ (B.44)

(See also Eq.$ \,$(C.1).) We see that the term $ SY\eta^\prime\eta^{\prime\prime}$ in the first equation above provides a mechanism for transverse waves to ``drive'' the generation of longitudinal waves. This coupling cannot be neglected if momentum effects are desired.

Physically, the rising edge of a transverse wave generates a longitudinal displacement in the direction of wave travel that propagates ahead at a much higher speed (typically an order of magnitude faster). The falling edge of the transverse wave then cancels this forward displacement as it passes by. See [391] for further details (including computer simulations).

Next Section:
Particle Velocity of a Gas
Previous Section:
Non-Stiff String