Young's Modulus as a Spring Constant
Recall (§B.1.3) that Hooke's Law defines a spring
constant ![]() as the applied force
as the applied force ![]() divided by the spring
displacement
divided by the spring
displacement ![]() , or
, or ![]() . An elastic solid can be viewed as a
bundle of ideal springs. Consider, for example, an ideal
bar (a rectangular solid in which one dimension, usually its
longest, is designated its length
. An elastic solid can be viewed as a
bundle of ideal springs. Consider, for example, an ideal
bar (a rectangular solid in which one dimension, usually its
longest, is designated its length ![]() ), and consider compression by
), and consider compression by
![]() along the length dimension. The length of each spring in
the bundle is the length of the bar, so that each spring constant
along the length dimension. The length of each spring in
the bundle is the length of the bar, so that each spring constant ![]() must be inversely proportional to
must be inversely proportional to ![]() ; in particular, each doubling of
length
; in particular, each doubling of
length ![]() doubles the length of each ``spring'' in the bundle, and
therefore halves its stiffness. As a result, it is useful to
normalize displacement
doubles the length of each ``spring'' in the bundle, and
therefore halves its stiffness. As a result, it is useful to
normalize displacement ![]() by length
by length ![]() and use relative
displacement
and use relative
displacement
![]() . We need displacement per unit length
because we have a constant spring compliance per unit length.
. We need displacement per unit length
because we have a constant spring compliance per unit length.
The number of springs in parallel is proportional to the
cross-sectional area ![]() of the bar. Therefore, the force applied to
each spring is proportional to the total applied force
of the bar. Therefore, the force applied to
each spring is proportional to the total applied force ![]() divided by
the cross-sectional area
divided by
the cross-sectional area ![]() . Thus, Hooke's law for each spring in the
bundle can be written
. Thus, Hooke's law for each spring in the
bundle can be written
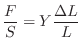
We may say that Young's modulus is the Hooke's-law spring constant for the spring made from a specifically cut section of the solid material, cut to length 1 and cross-sectional area 1. The shape of the cross-sectional area does not matter since all displacement is assumed to be longitudinal in this model.
Next Section:
Frequency-Dependent Losses
Previous Section:
Examples




















