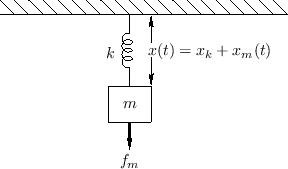
Hooke's Law
Consider an ideal spring suspending a mass from a rigid ceiling, as
depicted in Fig.B.1. Assume the mass is at rest,
and that its distance ![]() from the ceiling is fixed.
from the ceiling is fixed.
If ![]() denotes the mass of the earth, and
denotes the mass of the earth, and ![]() is the distance of mass
is the distance of mass
![]() 's center from the earth's center of mass, then the downward force
on the mass
's center from the earth's center of mass, then the downward force
on the mass ![]() is given by Eq.
is given by Eq.![]() (B.2) as
(B.2) as
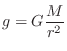
where
Note that the force on the spring in Fig.B.1 is gravitational force. Equal and opposite to the force of gravity is the spring force exerted upward by the spring on the mass (which is not moving). We know that the spring force is equal and opposite to the gravitational force because the mass would otherwise be accelerated by the net force.B.4 Therefore, like gravity, a displaced spring can be regarded as a definition of an applied force. That is, whenever you have to think of an applied force, you can always consider it as being delivered by the end of some ideal spring attached to some external physical system.
Note, by the way, that normal interaction forces when objects touch arise from the Coulomb force (electrostatic force, or repulsion of like charges) between electron orbitals. This electrostatic force obeys an ``inverse square law'' like gravity, and therefore also behaves like an ideal spring for small displacements.B.5
The specific value of ![]() depends on the physical units adopted as
well as the ``stiffness'' of the spring. What is most important in
this definition of force is that a doubling of spring displacement
doubles the force. That is, the spring force is a linear
function of spring displacement (compression or stretching).
depends on the physical units adopted as
well as the ``stiffness'' of the spring. What is most important in
this definition of force is that a doubling of spring displacement
doubles the force. That is, the spring force is a linear
function of spring displacement (compression or stretching).
Next Section:
Applying Newton's Laws of Motion
Previous Section:
Gravitational Force