DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Bartlett (``Triangular'') Window

The Bartlett window (or simply triangular window) may be defined by

$\displaystyle w(n) = w_R(n)\left[1 - \frac{\vert n\vert}{\frac{M-1}{2}}\right], \quad n\in\left[-\frac{M-1}{2},\frac{M-1}{2}\right]$ (4.31)

and the corresponding transform is

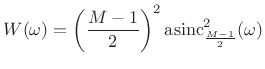$\displaystyle W(\omega) = \left(\frac{M-1}{2}\right)^2\hbox{asinc}_{\frac{M-1}{2}}^2(\omega)$ (4.32)

The following properties are immediate:

  • Convolution of two length 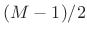$ (M-1)/2$ rectangular windows
  • Main lobe twice as wide as that of a rectangular window of length $ M$
  • First side lobe twice as far down as rectangular case (-26 dB)
  • Often applied implicitly to sample correlations of finite data
  • Also called the ``tent function''
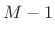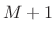  • Can replace $ M-1$ by $ M+1$ to avoid including endpoint zeros

Matlab for the Bartlett Window:

In matlab, a length $ M$ Bartlett window is designed by the statement

w = bartlett(M);
This is equivalent, for odd $ M$ , to 
w = 2*(0:(M-1)/2)/(M-1);
w = [w w((M-1)/2:-1:1)]';
Note that, in contrast to the hanning function, but like the hann function, bartlett explicitly includes zeros at its endpoints:
>> bartlett(3)
ans =
     0
     1
     0
The triang function in Matlab implements the triangular window corresponding to the hanning case:
>> triang(3)
ans =
     0.5000
     1.0000
     0.5000

Next Section:
Poisson Window
Previous Section:
Spectrum Analysis of an Oboe Tone