Free Books
   Free Books    Spectral Audio Signal Processing  

Poisson Window

The Poisson window (or more generically exponential window) can be written

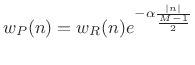$\displaystyle w_P(n) = w_R(n)e^{- \alpha \frac{\vert n\vert}{ \frac{M-1}{2} }}$ (4.33)

where $ \alpha $ determines the time constant $ \tau$ :

$\displaystyle \frac{\tau}{T} = \frac{M-1}{2\alpha}\quad\hbox{samples}$ (4.34)

where $ T$ denotes the sampling interval in seconds.

Figure 3.19: The Poisson (exponential) window.
\includegraphics[width=3.5in]{eps/poissonwindow}

The Poisson window is plotted in Fig.3.19. In the $ z$ plane, the Poisson window has the effect of radially contracting the unit circle. Consider an infinitely long Poisson window (no truncation by a rectangular window $ w_R$ ) applied to a causal signal $ h(n)$ having $ z$ transform $ H(z)$ :

\begin{eqnarray*} H_P(z) &=& \sum_{n=0}^\infty [w(n)h(n)] z^{-n} \\ &=& \sum_{n=0}^\infty \left[h(n) e^{- \frac{ \alpha n}{ M/2 }}\right] z^{-n} \qquad\hbox{(let $r\isdef e^{-\frac{\alpha}{ M/2 }}$)}\\ &=& \sum_{n=0}^\infty h(n) z^{-n} r^{n} = \sum_{n=0}^\infty h(n) (z/r)^{-n} \\ &=& H\left(\frac{z}{r}\right) \end{eqnarray*}

Thus, the unit-circle response is moved to $ \vert z\vert=1/r$ . This means, for example, that marginally stable poles in $ H(z)$ now decay as $ r^{-n}=e^{-\alpha n/(M/2)}$ in $ H(zr)$ .

The effect of this radial $ z$ -plane contraction is shown in Fig.3.20.

Figure 3.20: Radial contraction of the unit circle in the $ z$ plane by the Poisson window.
\includegraphics[width=3.5in]{eps/zplane2}

The Poisson window can be useful for impulse-response modeling by poles and/or zeros (``system identification''). In such applications, the window length is best chosen to include substantially all of the impulse-response data.

Next Section:
Hann-Poisson Window
Previous Section:
Bartlett (``Triangular'') Window