Free Books    Spectral Audio Signal Processing  

Downsampling and Aliasing

The downsampling operator $ \hbox{\sc Downsample}_M$ selects every $ M^{th}$ sample of a signal:

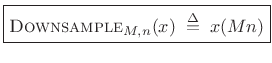$\displaystyle \zbox {\hbox{\sc Downsample}_{M,n}(x) \isdefs x(Mn)}$ (3.32)

The aliasing theorem states that downsampling in time corresponds to aliasing in the frequency domain:

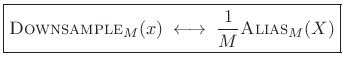$\displaystyle \zbox {\hbox{\sc Downsample}_M(x) \;\longleftrightarrow\;\frac{1}{M} \hbox{\sc Alias}_M(X)}$ (3.33)

where the $ \hbox{\sc Alias}$ operator is defined as

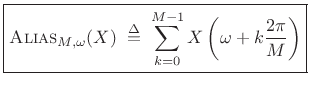$\displaystyle \zbox {\hbox{\sc Alias}_{M,\omega}(X) \isdefs \sum_{k=0}^{M-1} X\left(\omega+k\frac{2\pi}{M}\right)}$ (3.34)

for $ \omega\in[-\pi,\pi)$ . The summation terms for $ k\neq 0$ are called aliasing components.

In z transform notation, the $ \hbox{\sc Alias}$ operator can be expressed as [287]

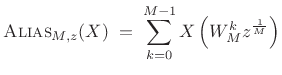$\displaystyle \hbox{\sc Alias}_{M,z}(X) \eqsp \sum_{k=0}^{M-1} X\left(W_M^k z^\frac{1}{M}\right)$ (3.35)

where $ W_M\isdeftext e^{j2\pi/M}$ is a common notation for the primitive $ M$ th root of unity. On the unit circle of the $ z$ plane, this becomes

$\displaystyle \hbox{\sc Alias}_{M,\omega}(X) \eqsp \sum_{k=0}^{M-1} X\left[e^{j\left(\frac{\omega}{M} + k\frac{2\pi}{M}\right)}\right], \quad -\pi\leq \omega < \pi.$ (3.36)

The frequency scaling corresponds to having a sampling interval of $ T=1$ after downsampling, which corresponds to the interval $ T=1/M$ prior to downsampling.

The aliasing theorem makes it clear that, in order to downsample by factor $ M$ without aliasing, we must first lowpass-filter the spectrum to $ (-\pi / M, \pi / M)$ . This filtering (when ideal) zeroes out the spectral regions which alias upon downsampling.

Note that any rational sampling-rate conversion factor $ \rho = L/M$ may be implemented as an upsampling by the factor $ L$ followed by downsampling by the factor $ M$ [50,287]. Conceptually, a stretch-by-$ L$ is followed by a lowpass filter cutting off at $ \omega_c \isdeftext \pi/(L\;\max\;M)$ , followed by downsample-by-$ L$ , i.e.,

$\displaystyle x^\prime \eqsp \hbox{\sc Downsample}_M\{\hbox{\sc Lowpass}_{\omega_c}[\hbox{\sc Stretch}_L(x)]\}$ (3.37)

In practice, there are more efficient algorithms for sampling-rate conversion [270,135,78] based on a more direct approach to bandlimited interpolation.

Proof of Aliasing Theorem

To show:

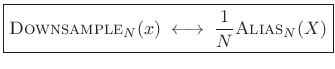
$\displaystyle \zbox {\hbox{\sc Downsample}_N(x) \;\longleftrightarrow\;\frac{1}{N} \hbox{\sc Alias}_N(X)} $

or
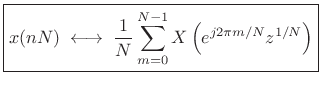
\fbox{$x(nN) \;\longleftrightarrow\;\dfrac{1}{N} \displaystyle\sum_{m=0}^{N-1} X\left(e^{j2\pi m/N} z^{1/N}\right)$}

From the DFT case [264], we know this is true when $ x$ and $ X$ are each complex sequences of length $ N_s$ , in which case $ y$ and $ Y$ are length $ N_s/N$ . Thus,

$\displaystyle x(nN) \;\longleftrightarrow\; Y(\omega_k N) \eqsp \frac{1}{N} \sum_{m=0}^{N-1} X\left(\omega_k + \frac{2\pi}{N} m \right), \; k\in [0,N_s/N)$ (3.38)

where we have chosen to keep frequency samples $ \omega_k$ in terms of the original frequency axis prior to downsampling, i.e., $ \omega_k = 2\pi k/ N_s$ for both $ X$ and $ Y$ . This choice allows us to easily take the limit as $ N_s\to\infty$ by simply replacing $ \omega_k$ by $ \omega$ :

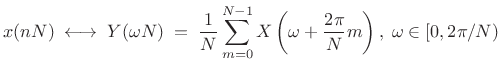$\displaystyle x(nN) \;\longleftrightarrow\; Y(\omega N) \eqsp \frac{1}{N} \sum_{m=0}^{N-1} X\left(\omega + \frac{2\pi}{N} m \right), \; \omega\in[0,2\pi/N)$ (3.39)

Replacing $ \omega$ by $ \omega^\prime =\omega N$ and converting to $ z$ -transform notation $ X(z)$ instead of Fourier transform notation $ X(\omega)$ , with $ z=e^{j\omega^\prime }$ , yields the final result.

Next Section:
Differentiation Theorem Dual
Previous Section:
Stretch/Repeat (Scaling) Theorem