Free Books    Spectral Audio Signal Processing  


Dyadic Filter Banks

Figure 11.34: Frequency response magnitudes for a dyadic filter bank (amplitude scalings optional).
\includegraphics[width=0.7\twidth]{eps/dyadicFilters}

A dyadic filter bank is any octave filter bank,12.6 as illustrated qualitatively in Figure 11.34. Note that $ H_0(\omega )$ is the top-octave bandpass filter, $ H_1(w) = \sqrt{2} H_0(2\omega )$ is the bandpass filter for next octave down, $ H_2(w) = 2H_0(4\omega )$ is the octave bandpass below that, and so on. The optional scale factors result in the same sum-of-squares for each channel-filter impulse response.

A dyadic filter bank may be derived from the discrete wavelet filter bank by setting $ a=2$ and relaxing the exact orthonormality requirement on the channel-filter impulse responses. If they do happen to be orthonormal, we may call it a dyadic wavelet filter bank.

For a dyadic filter bank, the center-frequency of the $ k$ th channel-filter impulse response can be defined as

$\displaystyle \omega _c(k) \eqsp \sqrt{\omega _0(\omega _0+\hbox{bandwidth})} \eqsp \sqrt{2}\omega _0$ (12.123)

so that

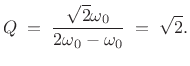$\displaystyle Q \eqsp \frac{\sqrt{2}\omega _0}{2\omega _0 - \omega _0} \eqsp \sqrt{2}.$ (12.124)

Thus, a dyadic filter bank is a special case of a constant-Q filter bank for which the $ Q$ is $ \sqrt{2}$ .

Next Section:
Dyadic Filter Bank Design
Previous Section:
Discrete Wavelet Filterbank