DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Discrete Wavelet Filterbank

In a discrete wavelet filterbank, each basis signal is interpreted as the impulse response of a bandpass filter in a constant-Q filter bank:

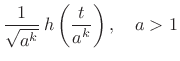$\displaystyle h_k(t)$ $\displaystyle =$ $\displaystyle \frac{1}{\sqrt{a^k}}\, h\left(\frac{t}{a^k}\right), \quad a>1$  
$\displaystyle \longleftrightarrow\quad H_k(\omega )$ $\displaystyle =$ $\displaystyle \sqrt{a^k}\, H(a^k\omega )$  

Thus, the $ k$ th channel-filter $ H_k(\omega )$ is obtained by frequency-scaling (and normalizing for unit energy) the zeroth channel filter $ H_0(\omega )$ . The frequency scale-factor is of course equal to the inverse of the time-scale factor.

Recall that in the STFT, channel filter $ H_k(\omega )$ is a shift of the zeroth channel-filter $ H_0(\omega )$ (which corresponds to ``cosine modulation'' in the time domain).

As the channel-number $ k$ increases, the channel impulse response $ h_k$ lengthens by the factor $ a^k$ ., while the pass-band of its frequency-response $ H_k$ narrows by the inverse factor $ a^{-k}$ .

Figure 11.32 shows a block diagram of the discrete wavelet filter bank for $ a=2$ (the ``dyadic'' or ``octave filter-bank'' case), and Fig.11.33 shows its time-frequency tiling as compared to that of the STFT. The synthesis filters $ f_k$ may be used to make a biorthogonal filter bank. If the $ h_k$ are orthonormal, then $ f_k=h_k$ .

Figure 11.32: Dyadic Biorthogonal Wavelet Filterbank
\includegraphics[width=\twidth]{eps/DyadicFilterbank}

Figure 11.33: Time-frequency tiling for the Short-Time Fourier Transform (left) and dyadic wavelet filter bank (right).
\includegraphics[width=0.8\twidth]{eps/DyadicTiling}

Next Section:
Dyadic Filter Banks
Previous Section:
Discrete Wavelet Transform