DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Example: Random Bit String

Consider a random sequence of 1s and 0s, i.e., the probability of a 0 or 1 is always $ P(0)=P(1)=1/2$ . The corresponding probability density function is

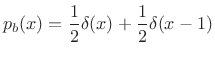$\displaystyle p_b(x) = \frac{1}{2}\delta(x) + \frac{1}{2}\delta(x-1)$ (D.31)

and the entropy is

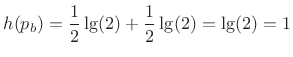$\displaystyle h(p_b) = \frac{1}{2}\lg(2) + \frac{1}{2}\lg(2) = \lg(2) = 1$ (D.32)

Thus, 1 bit is required for each bit of the sequence. In other words, the sequence cannot be compressed. There is no redundancy.

If instead the probability of a 0 is 1/4 and that of a 1 is 3/4, we get

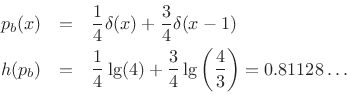
\begin{eqnarray*} p_b(x) &=& \frac{1}{4}\delta(x) + \frac{3}{4}\delta(x-1)\\ h(p_b) &=& \frac{1}{4}\lg(4) + \frac{3}{4}\lg\left(\frac{4}{3}\right) = 0.81128\ldots \end{eqnarray*}

and the sequence can be compressed about $ 19\%$ .

In the degenerate case for which the probability of a 0 is 0 and that of a 1 is 1, we get

\begin{eqnarray*} p_b(x) &=& \lim_{\epsilon \to0}\left[\epsilon \delta(x) + (1-\epsilon )\delta(x-1)\right]\\ h(p_b) &=& \lim_{\epsilon \to0}\epsilon \cdot\lg\left(\frac{1}{\epsilon }\right) + 1\cdot\lg(1) = 0. \end{eqnarray*}

Thus, the entropy is 0 when the sequence is perfectly predictable.

Next Section:
Maximum Entropy Distributions
Previous Section:
Entropy of a Probability Distribution