DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Maximum Entropy Distributions

Uniform Distribution

Among probability distributions $ p(x)$ which are nonzero over a finite range of values $ x\in[a,b]$ , the maximum-entropy distribution is the uniform distribution. To show this, we must maximize the entropy,

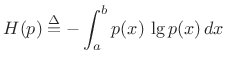$\displaystyle H(p) \isdef -\int_a^b p(x)\, \lg p(x)\, dx$ (D.33)

with respect to $ p(x)$ , subject to the constraints

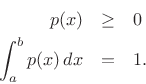
\begin{eqnarray*} p(x) &\geq& 0\\ \int_a^b p(x)\,dx &=& 1. \end{eqnarray*}

Using the method of Lagrange multipliers for optimization in the presence of constraints [86], we may form the objective function

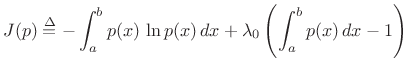$\displaystyle J(p) \isdef -\int_a^b p(x) \, \ln p(x) \,dx + \lambda_0\left(\int_a^b p(x)\,dx - 1\right)$ (D.34)

and differentiate with respect to $ p(x)$ (and renormalize by dropping the $ dx$ factor multiplying all terms) to obtain

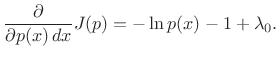$\displaystyle \frac{\partial}{\partial p(x)\,dx} J(p) = - \ln p(x) - 1 + \lambda_0.$ (D.35)

Setting this to zero and solving for $ p(x)$ gives

$\displaystyle p(x) = e^{\lambda_0-1}.$ (D.36)

(Setting the partial derivative with respect to $ \lambda_0$ to zero merely restates the constraint.)

Choosing $ \lambda_0$ to satisfy the constraint gives $ \lambda_0 =1-\ln(b-a)$ , yielding

$\displaystyle p(x) = \left\{\begin{array}{ll} \frac{1}{b-a}, & a\leq x \leq b \\ [5pt] 0, & \hbox{otherwise}. \\ \end{array} \right.$ (D.37)

That this solution is a maximum rather than a minimum or inflection point can be verified by ensuring the sign of the second partial derivative is negative for all $ x$ :

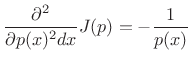$\displaystyle \frac{\partial^2}{\partial p(x)^2dx} J(p) = - \frac{1}{p(x)}$ (D.38)

Since the solution spontaneously satisfied $ p(x)>0$ , it is a maximum.

Exponential Distribution

Among probability distributions $ p(x)$ which are nonzero over a semi-infinite range of values $ x\in[0,\infty]$ and having a finite mean $ \mu$ , the exponential distribution has maximum entropy.

To the previous case, we add the new constraint

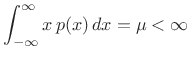$\displaystyle \int_{-\infty}^\infty x\,p(x)\,dx = \mu < \infty$ (D.39)

resulting in the objective function

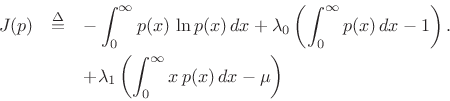
\begin{eqnarray*} J(p) &\isdef & -\int_0^\infty p(x) \, \ln p(x)\,dx + \lambda_0\left(\int_0^\infty p(x)\,dx - 1\right).\\ & & + \lambda_1\left(\int_0^\infty x\,p(x)\,dx - \mu\right) \end{eqnarray*}

Now the partials with respect to $ p(x)$ are

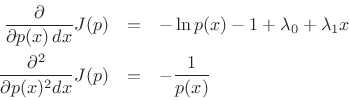
\begin{eqnarray*} \frac{\partial}{\partial p(x)\,dx} J(p) &=& - \ln p(x) - 1 + \lambda_0 + \lambda_1 x\\ \frac{\partial^2}{\partial p(x)^2 dx} J(p) &=& - \frac{1}{p(x)} \end{eqnarray*}

and $ p(x)$ is of the form $ p(x) = e^{(\lambda_0-1)+\lambda_1x}$ . The unit-area and finite-mean constraints result in $ \exp(\lambda_0-1) = 1/\mu$ and $ \lambda_1=-1/\mu$ , yielding

$\displaystyle p(x) = \left\{\begin{array}{ll} \frac{1}{\mu} e^{-x/\mu}, & x\geq 0 \\ [5pt] 0, & \hbox{otherwise}. \\ \end{array} \right.$ (D.40)

Gaussian Distribution

The Gaussian distribution has maximum entropy relative to all probability distributions covering the entire real line $ x\in(-\infty,\infty)$ but having a finite mean $ \mu$ and finite variance $ \sigma^2$ .

Proceeding as before, we obtain the objective function

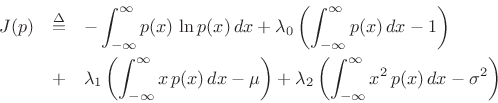
\begin{eqnarray*} J(p) &\isdef & -\int_{-\infty}^\infty p(x) \, \ln p(x)\,dx + \lambda_0\left(\int_{-\infty}^\infty p(x)\,dx - 1\right)\\ &+& \lambda_1\left(\int_{-\infty}^\infty x\,p(x)\,dx - \mu\right) + \lambda_2\left(\int_{-\infty}^\infty x^2\,p(x)\,dx - \sigma^2\right) \end{eqnarray*}

and partial derivatives

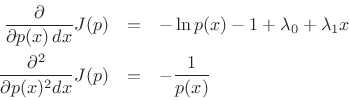
\begin{eqnarray*} \frac{\partial}{\partial p(x)\,dx} J(p) &=& - \ln p(x) - 1 + \lambda_0 + \lambda_1 x\\ \frac{\partial^2}{\partial p(x)^2 dx} J(p) &=& - \frac{1}{p(x)} \end{eqnarray*}

leading to

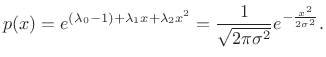$\displaystyle p(x) = e^{(\lambda_0-1)+\lambda_1 x + \lambda_2 x^2} = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{x^2}{2\sigma^2}}.$ (D.41)

For more on entropy and maximum-entropy distributions, see [48].

Next Section:
Gaussian Mean
Previous Section:
Example: Random Bit String