DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Expected Value


Definition: The expected value of a continuous random variable $ v\in(-\infty,\infty)$ is denoted $ E\{v\}$ and is defined by

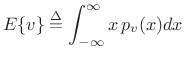$\displaystyle E\{v\} \isdef \int_{-\infty}^\infty x \, p_v(x) dx$ (C.12)

where $ p_v(x)$ denotes the probability density function (PDF) for the random variable v.


Example: Let the random variable $ v(n)$ be uniformly distributed between $ a$ and $ b$ , i.e.,

$\displaystyle p_v(x) = \left\{\begin{array}{ll} \frac{1}{b-a}, & a\leq x \leq b \\ [5pt] 0, & \hbox{otherwise}. \\ \end{array} \right.$ (C.13)

Then the expected value of $ v(n)$ is computed as

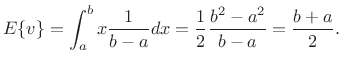$\displaystyle E\{v\} = \int_a^b x \frac{1}{b-a} dx = \frac{1}{2}\frac{b^2-a^2}{b-a} = \frac{b+a}{2}.$ (C.14)

Thus, the expected value of a random variable uniformly distributed between $ a$ and $ b$ is simply the average of $ a$ and $ b$ .

For a stochastic process, which is simply a sequence of random variables, $ E\{x(n)\}$ means the expected value of $ x(n)$ over ``all realizations'' of the random process $ x(\cdot)$ . This is also called an ensemble average. In other words, for each ``roll of the dice,'' we obtain an entire signal $ x(n),\, n=0,\pm1,\pm2,\cdots$ , and to compute $ E\{x(0)\}$ , say, we average together all of the values of $ x(0)$ obtained for all ``dice rolls.''

For a stationary random process $ x = \{x(n),\, n=0,\pm1,\pm2,\cdots\}$ , the random variables $ x(n)$ which make it up are identically distributed. As a result, we may normally compute expected values by averaging over time within a single realization of the random process, instead of having to average ``vertically'' at a single time instant over many realizations of the random process.C.2 Denote time averaging by

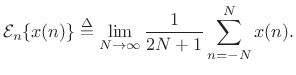$\displaystyle {\cal E}_n\{x(n)\} \isdef \lim_{N\to\infty}\frac{1}{2N+1}\sum_{n=-N}^N x(n).$ (C.15)

Then, for a stationary random processes, we have $ E\{x(n)\} = {\cal E}_n\{x(n)\}$ . That is, for stationary random signals, ensemble averages equal time averages.

We are concerned only with stationary stochastic processes in this book. While the statistics of noise-like signals must be allowed to evolve over time in high quality spectral models, we may require essentially time-invariant statistics within a single frame of data in the time domain. In practice, we choose our spectrum analysis window short enough to impose this. For audio work, 20 ms is a typical choice for a frequency-independent frame length.C.3 In a multiresolution system, in which the frame length can vary across frequency bands, several periods of the band center-frequency is a reasonable choice. As discussed in §5.5.2, the minimum number of periods required under the window for resolution of spectral peaks depends on the window type used.

Next Section:
Mean
Previous Section:
Stationary Stochastic Process