Mean
Definition:
The mean of a stochastic process 
at time 
is defined as
the expected value of
:
 |
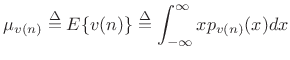(C.16) |
where
is the probability density function for the random
variable
.
For a stationary stochastic process 
, the mean is given by
the expected value of
for any
. I.e.,
for all
.
Next Section:
Sample Mean
Previous Section:
Expected Value
