Free Books
   Free Books    Spectral Audio Signal Processing  

Gaussian Central Moments

The characteristic function of a zero-mean Gaussian is

$\displaystyle \Phi(\omega) = e^{-\frac{1}{2}\sigma^2\omega^2}$ (D.53)

Since a zero-mean Gaussian $ p(t)$ is an even function of $ t$ , (i.e., $ p(-t)=p(t)$ ), all odd-order moments $ m_i$ are zero. By the moment theorem, the even-order moments are

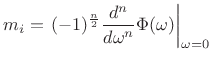$\displaystyle m_i = \left.(-1)^{\frac{n}{2}}\frac{d^n}{d\omega^n}\Phi(\omega)\right\vert _{\omega=0}$ (D.54)

In particular,

\begin{eqnarray*} \Phi^\prime(\omega) &=& -\frac{1}{2}\sigma^2 2\omega\Phi(\omega)\\ [5pt] \Phi^{\prime\prime}(\omega) &=& -\frac{1}{2}\sigma^2 2\omega\Phi^\prime(\omega) -\frac{1}{2}\sigma^2 2\Phi(\omega) \end{eqnarray*}

Since $ \Phi(0)=1$ and $ \Phi^\prime(0)=0$ , we see $ m_1=0$ , $ m_2=\sigma^2$ , as expected.

Next Section:
Computing
Previous Section:
Gaussian Characteristic Function