Gaussian Characteristic Function
Since the Gaussian PDF is
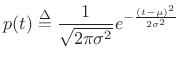 |
(D.50) |
and since the Fourier transform of
| (D.51) |
It follows that the Gaussian characteristic function is
| (D.52) |
Next Section:
Gaussian Central Moments
Previous Section:
Moment Theorem
Since the Gaussian PDF is
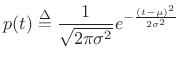 |
(D.50) |
| (D.51) |
| (D.52) |




