DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Gaussian Mean

The mean of a distribution $ f(t)$ is defined as its first-order moment:

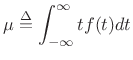$\displaystyle \mu \isdef \int_{-\infty}^\infty t f(t)dt$ (D.42)

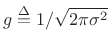To show that the mean of the Gaussian distribution is $ \mu$ , we may write, letting $ g\isdef 1/\sqrt{2\pi\sigma^2}$ ,

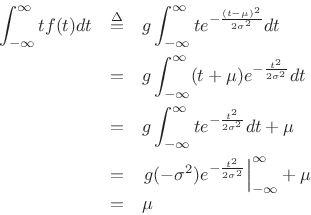
\begin{eqnarray*} \int_{-\infty}^\infty t f(t) dt &\isdef & g \int_{-\infty}^\infty t e^{-\frac{(t-\mu)^2}{2\sigma^2}} dt\\ &=&g \int_{-\infty}^\infty (t+\mu) e^{-\frac{t^2}{2\sigma^2}} dt\\ &=&g \int_{-\infty}^\infty t e^{-\frac{t^2}{2\sigma^2}} dt + \mu\\ &=&\left.g(-\sigma^2) e^{-\frac{t^2}{2\sigma^2}} \right\vert _{-\infty}^{\infty} + \mu\\ &=& \mu \end{eqnarray*}

since $ f(\pm\infty)=0$ .

Next Section:
Gaussian Variance
Previous Section:
Maximum Entropy Distributions