DSPRelated.com
Free Books
Online · Live + on demand
February 9-11, 2027
Price goes up Nov 1: register now to lock in today's rate
Register Now →
   Free Books    Spectral Audio Signal Processing  

Inverse DFT and the DFT Filter Bank Sum

The Length $ N$ inverse DFT is given by [264]

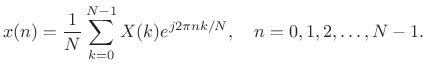$\displaystyle x(n) = \frac{1}{N}\sum_{k=0}^{N-1} X(k) e^{j2\pi nk/N}, \quad n=0,1,2,\ldots,N-1.$ (10.16)

This suggests that the DFT Filter Bank can be inverted by simply remodulating the baseband filter-bank signals $ y_k(n)$ , summing over $ k$ , and dividing by $ N$ for proper normalization. That is, we are led to conjecture that

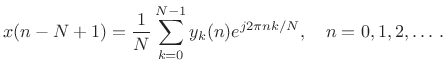$\displaystyle x(n-N+1) = \frac{1}{N}\sum_{k=0}^{N-1} y_k(n) e^{j2\pi nk/N}, \quad n=0,1,2,\ldots\,.$ (10.17)

This is in fact true, as we will later see. (It is straightforward to show as an exercise.)

Next Section:
Specific Windows
Previous Section:
DFT Filter Bank