Specific Windows
- Recall that the rectangular window transform is
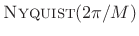 , implying the rectangular window itself is
, implying the rectangular window itself is
 ,
which is obvious.
,
which is obvious.
- The window transform for the Hamming family is
 ,
implying that Hamming windows are
,
implying that Hamming windows are
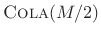 , which we also knew.
, which we also knew.
- The rectangular window transform is also
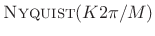 for any integer
for any integer
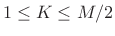 , implying that all hop sizes given
by
, implying that all hop sizes given
by 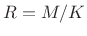 for
for
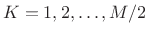 are COLA.
are COLA.
- Because its side lobes are the same width as the sinc side lobes,
the Hamming window transform is also
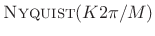 ,for any integer
,for any integer
 , implying hop sizes
, implying hop sizes 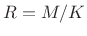 are good, for
are good, for
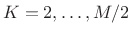 . Thus, the available hop sizes for the Hamming
window family include all of those for the rectangular window
except one (
. Thus, the available hop sizes for the Hamming
window family include all of those for the rectangular window
except one (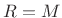 ).
).
Next Section:
The Nyquist Property on the Unit Circle
Previous Section:
Inverse DFT and the DFT Filter Bank Sum



















