Free Books
   Free Books    Spectral Audio Signal Processing  

Length L FIR Frame Filters

To avoid time aliasing, we restrict the filter length to a maximum of $ L$ samples. Since $ H_m(\omega_k)$ is an arbitrary multiplicative weighting of the $ m$ th spectral frame, the frame filter need not be causal. For odd $ L$ , the filter impulse response indices may run from $ -L_h$ to $ L_h$ , where

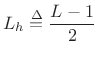$\displaystyle L_h \isdef \frac{L-1}{2}$ (9.43)

This gives

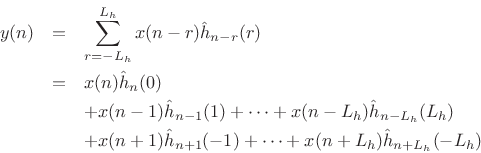
\begin{eqnarray*} y(n) &=& \sum_{r=-L_h}^{L_h} x(n-r) {\hat h}_{n-r}(r) \\ &=& x(n) {\hat h}_n(0) \\ & & + x(n-1) {\hat h}_{n-1}(1) + \cdots + x(n-L_h) {\hat h}_{n-L_h}(L_h) \\ & & + x(n+1) {\hat h}_{n+1}(-1) + \cdots + x(n+L_h) {\hat h}_{n+L_h}(-L_h) \end{eqnarray*}

This is the general length $ L$ time-varying FIR filter convolution sum for time $ n$ , when $ L$ is odd.

Next Section:
WOLA Processing Steps
Previous Section:
Block Diagram Interpretation of Time-Varying STFT Modifications