Block Diagram Interpretation of Time-Varying STFT Modifications

Free Books Spectral Audio Signal Processing

Block Diagram Interpretation of Time-Varying STFT Modifications

Assuming ${\hat h}$ is causal gives

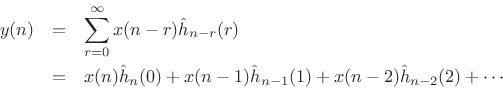
$\begin{eqnarray*} y(n) &=& \sum_{r=0}^\infty x(n-r) {\hat h}_{n-r}(r) \\ &=& x(n) {\hat h}_n(0) + x(n-1) {\hat h}_{n-1}(1) + x(n-2) {\hat h}_{n-2}(2) + \cdots \end{eqnarray*}$

This is depicted in Fig.8.17.

$\begin{psfrags} % latex2html id marker 23334\psfrag{zm1}{\large $z^{-1}$\ }\psfrag{h(0,n)}{\large$ h_n(0) $}\psfrag{h(1,n)}{\large$ h_{n-1}(1) $}\psfrag{h(2,n)}{\large$ h_{n-L+1}(L-1) $}\psfrag{+}{\large$\Sigma$}\psfrag{w(n)}{\large$ w $}\psfrag{y(n)}{\large$ y(n) $}\begin{figure}[htbp] \includegraphics[width=\twidth]{eps/olamods} \caption{System diagram giving an interpretation of the bandlimited time-varying filter coefficients in the overlap-add STFT processor with a new filter each frame.} \end{figure} \end{psfrags}$

The term can be interpreted as the FIR filter tap at time . Note how each tap is lowpass filtered by the FFT window . The window thus enforces bandlimiting each filter tap to the bandwidth of the window's main lobe. For an -term length- Blackman-Harris window, for example, the main-lobe reaches zero at frequency $L\Omega_M=2\pi L/M$ (see Table 5.2 in §5.5.2 for other examples). This bandlimiting places a limit on the bandwidth expansion caused by time-variation of the filter coefficients, which in turn places a limit on the maximum STFT hop-size that can be used without frequency-domain aliasing. See Allen and Rabiner 1977 [9] for further details on the bandlimiting property.