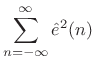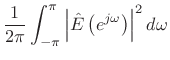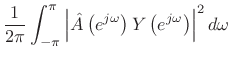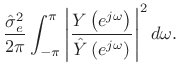DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Linear Prediction is Peak Sensitive

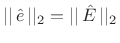By Rayleigh's energy theorem, $ \vert\vert\,{\hat e}\,\vert\vert _2= \vert\vert\,{\hat E}\,\vert\vert _2$ (as shown in §2.3.8). Therefore,

$\displaystyle \sum_{n=-\infty}^{\infty} {\hat e}^2(n)$ $\displaystyle =$ $\displaystyle \frac{1}{2\pi}\int_{-\pi}^{\pi}\left\vert{\hat E}\left(e^{j\omega}\right)\right\vert^2 d\omega$  
  $\displaystyle \isdef$ $\displaystyle \frac{1}{2\pi}\int_{-\pi}^{\pi}\left\vert{\hat A}\left(e^{j\omega}\right)Y\left(e^{j\omega}\right)\right\vert^2 d\omega$  
  $\displaystyle =$ $\displaystyle \frac{{\hat\sigma}^2_e}{2\pi}\int_{-\pi}^{\pi}\left\vert\frac{Y\left(e^{j\omega}\right)}% {{\hat Y}\left(e^{j\omega}\right)}\right\vert^2 d\omega. \protect$ (11.10)

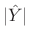
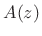
From this ``ratio error'' expression in the frequency domain, we can see that contributions to the error are smallest when $ \vert{\hat Y}(e^{j\omega})\vert>\vert Y(e^{j\omega})\vert$ . Therefore, LP tends to overestimate peaks. LP cannot make $ \vert{\hat Y}\vert$ arbitrarily large because $ A(z)$ is constrained to be monic and minimum-phase. 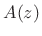It can be shown that the log-magnitude frequency response of every minimum-phase monic polynomial $ A(z)$ is zero-mean [162]. Therefore, for each peak overestimation, there must be an equal-area ``valley underestimation'' (in a log-magnitude plot over the unit circle).

Next Section:
Linear Prediction Methods
Previous Section:
Points to Note