Points to Note

We saw that in OLA with time varying modifications and 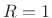(a ``sliding'' DFT), the window served as a lowpass filter on each individual tap of the FIR filter being implemented.
In the more typical case in which is the window length divided by a small integer like 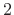- 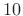, we may think of the window as specifying a type of cross-fade from the LTI filter for one frame to the LTI filter for the next frame.
Using a Bartlett (triangular) window with 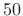% overlap, (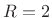 ), the sequence of FIR filters used is obtained simply by linearly interpolating the LTI filter for one frame to the LTI filter for the next.
In FBS, there is no limitation on how fast the filter may vary with time, but its length is limited to that of the window .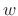
In OLA, there is no limit on length (just add more zero-padding), but the filter taps are band-limited to the spectral width of the window.
FBS filters are time-limited 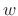by , while OLA filters are band-limited by 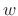(another dual relation).
Recall for comparison that each frame in the OLA method is filtered according to

$\displaystyle Y_m = X_m \cdot H_m = [X*W_m] \cdot H_m \;\longleftrightarrow\; \underbrace{[x \cdot w_m]}_{x_m} * h_m$ (10.34)

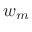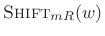where denotes $\hbox{\sc Shift}_{mR}(w)$ .
Time-varying FBS filters are instantly in ``steady state''
FBS filters must be changed very slowly to avoid clicks and pops (discontinuity distortion is likely when the filter changes)