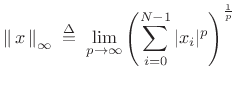Lp norms
The ![]() norm of an
norm of an ![]() -dimensional vector (signal)
-dimensional vector (signal) ![]() is defined as
is defined as
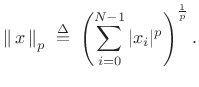 |
(5.27) |
Special Cases
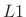 norm
norm

(5.28)
- Sum of the absolute values of the elements
- ``City block'' distance
 norm
norm
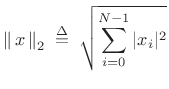
(5.29)
- ``Euclidean'' distance
- Minimized by ``Least Squares'' techniques
-
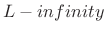 norm
norm
In the limit as
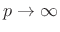 , the
, the 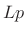 norm of
norm of  is dominated by the maximum element of
is dominated by the maximum element of  . Optimal Chebyshev
filters minimize this norm of the frequency-response error.
. Optimal Chebyshev
filters minimize this norm of the frequency-response error.
Filter Design using Lp Norms
Formulated as an ![]() norm minimization, the FIR filter design problem
can be stated as follows:
norm minimization, the FIR filter design problem
can be stated as follows:
| (5.31) |
where
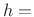 FIR filter coefficients
FIR filter coefficients
-
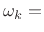 suitable discrete set of frequencies
suitable discrete set of frequencies
-
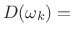 desired (complex) frequency response
desired (complex) frequency response
-
 obtained frequency response (typically fft(h))
obtained frequency response (typically fft(h))
-
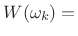 (optional) error weighting function
(optional) error weighting function
Next Section:
Optimal Chebyshev FIR Filters
Previous Section:
Conclusions